题目内容
 如图,平面上有四个点,它们的坐标分别是A(2,-2
如图,平面上有四个点,它们的坐标分别是A(2,-2 )、B(5,-2
)、B(5,-2 )、C(5,-
)、C(5,- )、D(2,-
)、D(2,- ).
).
(1)顺次连接A、B、C、D,围成的四边形是什么图形?
(2)求这个四边形的面积是多少?
(3)将这个四边形向上平移 个单位长度,四个顶点的坐标变为多少?
个单位长度,四个顶点的坐标变为多少?
解:(1)围成的四边形ABCD是矩形,
理由是:∵A(2,-2 )、B(5,-2
)、B(5,-2 )、C(5,-
)、C(5,- )、D(2,-
)、D(2,- ),
),
∴AD∥BC∥y轴,DC∥AB∥x轴,
∴AD⊥DC,
∴四边形ABCD是矩形;
(2)∵A(2,-2 )、B(5,-2
)、B(5,-2 )、C(5,-
)、C(5,- )、D(2,-
)、D(2,- ),
),
∴AB=5-2=3,AD=- -(-2
-(-2 )=
)= ,
,
∴矩形ABCD的面积是AB×AD=3 ;
;
(3)∵A(2,-2 )、B(5,-2
)、B(5,-2 )、C(5,-
)、C(5,- )、D(2,-
)、D(2,- ),
),
∴将这个四边形向上平移 个单位长度,四个顶点的坐标变为A(2,-
个单位长度,四个顶点的坐标变为A(2,- ),B(5,-
),B(5,- ),C(5,0),D(2,0).
),C(5,0),D(2,0).
分析:(1)根据点的坐标得出AD∥BC∥y轴,DC∥AB∥x轴推出AD⊥DC,根据矩形的判定得出四边形是矩形;
(2)求出AB、AD,即可求出矩形的面积;
(3)根据平移性质把各个点的纵坐标加上 即可得出答案.
即可得出答案.
点评:本题考查了矩形的现在和判定,平移的性质,关键是能熟练地运用性质进行计算.
理由是:∵A(2,-2
 )、B(5,-2
)、B(5,-2 )、C(5,-
)、C(5,- )、D(2,-
)、D(2,- ),
),∴AD∥BC∥y轴,DC∥AB∥x轴,
∴AD⊥DC,
∴四边形ABCD是矩形;
(2)∵A(2,-2
 )、B(5,-2
)、B(5,-2 )、C(5,-
)、C(5,- )、D(2,-
)、D(2,- ),
),∴AB=5-2=3,AD=-
 -(-2
-(-2 )=
)= ,
,∴矩形ABCD的面积是AB×AD=3
 ;
;(3)∵A(2,-2
 )、B(5,-2
)、B(5,-2 )、C(5,-
)、C(5,- )、D(2,-
)、D(2,- ),
),∴将这个四边形向上平移
 个单位长度,四个顶点的坐标变为A(2,-
个单位长度,四个顶点的坐标变为A(2,- ),B(5,-
),B(5,- ),C(5,0),D(2,0).
),C(5,0),D(2,0).分析:(1)根据点的坐标得出AD∥BC∥y轴,DC∥AB∥x轴推出AD⊥DC,根据矩形的判定得出四边形是矩形;
(2)求出AB、AD,即可求出矩形的面积;
(3)根据平移性质把各个点的纵坐标加上
 即可得出答案.
即可得出答案.点评:本题考查了矩形的现在和判定,平移的性质,关键是能熟练地运用性质进行计算.

练习册系列答案
相关题目

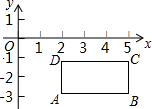 如图,平面上有四个点,它们的坐标分别是A(2,-2
如图,平面上有四个点,它们的坐标分别是A(2,-2 如图,平面上有四个点A、B、C、D,按下列要求画出图形:(不写作法,保留作图痕迹)
如图,平面上有四个点A、B、C、D,按下列要求画出图形:(不写作法,保留作图痕迹) 画图题:
画图题: 如图,平面上有四个点A,B,C,D,按下列要求画出图形.
如图,平面上有四个点A,B,C,D,按下列要求画出图形.