题目内容
 直线AB与双曲线y=
直线AB与双曲线y=| k |
| x |
(1)求直线AB的解析式;
(2)经过点D(1,0)的直线DE与y轴交于点E,且与直线AB交于点F,连接BD.
①若E点的坐标为(0,-
| 3 |
| 2 |
②若E点在y轴上运动,坐标为(0,m).设△BDF的面积为S,当m<3时,请直接写出S关于m的函数关系式.
分析:(1)首先利用待定系数法求得双曲线的解析式,根据A在双曲线上,求得A的坐标,然后利用待定系数法即可求得直线AB的解析式;
(2)①首先利用待定系数法求得直线DE的解析式,解方程组即可求得点F的坐标,然后根据S△BDF=S△BEF+S△BDF,即可求解;
②与①的解法相同即可利用m表示出S的值,从而得到S关于m的函数关系式.
(2)①首先利用待定系数法求得直线DE的解析式,解方程组即可求得点F的坐标,然后根据S△BDF=S△BEF+S△BDF,即可求解;
②与①的解法相同即可利用m表示出S的值,从而得到S关于m的函数关系式.
解答: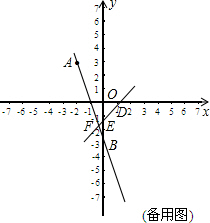 解:(1)把C(-1,6)代入y=
解:(1)把C(-1,6)代入y=
得:
6=
,解得:k=-6.
则双曲线的解析式是:y=-
.
把A(-2,n)代入得:n=-
=3,
则A的坐标是:(-2,3).
设直线AB的解析式是:y=kx+b,
根据题意得:
,
解得:
.
则直线AB的解析式是:y=-3x-3;
(2)①设直线DE的解析式是:y=mx+n,
根据题意得:
,
解得:
,
则直线DE的解析式是:y=
x-
.
解方程组:
,
解得:
.
则F的坐标是:(-
,-1).BF=
.
则S△BDF=S△BEF+S△BDF=
×
×
+
×
×1=
;
②S=
.
 解:(1)把C(-1,6)代入y=
解:(1)把C(-1,6)代入y=| k |
| x |
6=
| k |
| -1 |
则双曲线的解析式是:y=-
| 6 |
| x |
把A(-2,n)代入得:n=-
| 6 |
| -2 |
则A的坐标是:(-2,3).
设直线AB的解析式是:y=kx+b,
根据题意得:
|
解得:
|
则直线AB的解析式是:y=-3x-3;
(2)①设直线DE的解析式是:y=mx+n,
根据题意得:
|
解得:
|
则直线DE的解析式是:y=
| 3 |
| 2 |
| 3 |
| 2 |
解方程组:
|
解得:
|
则F的坐标是:(-
| 1 |
| 3 |
| 8 |
| 3 |
则S△BDF=S△BEF+S△BDF=
| 1 |
| 2 |
| 8 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
| 16 |
| 9 |
②S=
| 3(m+3) |
| 3-m |
点评:本题考查了反比例函数的综合运用.关键是根据利用待定系数法求函数解析式,求函数图象的交点坐标.

练习册系列答案
相关题目
 如图,直线AB与双曲线的一个交点为点C,CD⊥x轴与点D,OD=2OB=4OA=4. 求一次函数和反比例函数的解析式.
如图,直线AB与双曲线的一个交点为点C,CD⊥x轴与点D,OD=2OB=4OA=4. 求一次函数和反比例函数的解析式.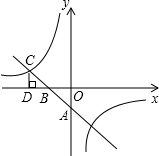 如图,一次函数与反比例函数的图象分别是直线AB和双曲线.直线AB与双曲线的一个交点为点C,CD⊥x轴于点D,OD=2OB=4OA=4.此一次函数的解析式为
如图,一次函数与反比例函数的图象分别是直线AB和双曲线.直线AB与双曲线的一个交点为点C,CD⊥x轴于点D,OD=2OB=4OA=4.此一次函数的解析式为 如图,直线与y=2x双曲线
如图,直线与y=2x双曲线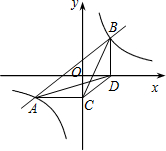 如图,直线AB与双曲线y=
如图,直线AB与双曲线y=