题目内容
定义:a是不等于1的有理数,我们把
称为a的差倒数.如:2的差倒数是
=-1,-1的差倒数是
=
.已知a1=-
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,以此类推,则a2011=
| 1 |
| 1-a |
| 1 |
| 1-2 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
| 1 |
| 5 |
-
| 1 |
| 5 |
-
.| 1 |
| 5 |
分析:根据“差倒数”的定义求出前几个数,便不难发现,每三个数为一个循环组依次循环,然后用2011÷3,根据余数的情况确定a2011的值.
解答:解:a2=
=
,
a3=
=6,
a4=
=-
,
…,
依此类推,每三个数为一个循环组依次循环,
∵2011÷3=670余1,
∴a2011与a1相同,为-
.
故答案为:-
.
| 1 | ||
1-(-
|
| 5 |
| 6 |
a3=
| 1 | ||
1-
|
a4=
| 1 |
| 1-6 |
| 1 |
| 5 |
…,
依此类推,每三个数为一个循环组依次循环,
∵2011÷3=670余1,
∴a2011与a1相同,为-
| 1 |
| 5 |
故答案为:-
| 1 |
| 5 |
点评:本题是对数字变化规律的考查,理解“差倒数”的定义并求出每三个数为一个循环组依次循环是解题的关键.

练习册系列答案
相关题目
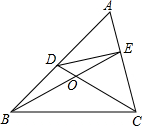 述条件的图形中是否存在等对边四边形,并证明你的结论.
述条件的图形中是否存在等对边四边形,并证明你的结论. 称为a的差倒数,如:2的差倒数是
称为a的差倒数,如:2的差倒数是 ,-1的差倒数是
,-1的差倒数是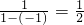 ,已知
,已知 ,
, ,…,
,…, …×
…× ,试根据上面规律,
,试根据上面规律, …
… .
.