Question

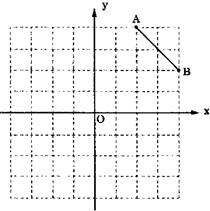
己知平面直角坐标系上的三个点O（0，0）、A（-2，2）、B（-2，0），将△ABO绕O按顺时针方向旋转135°，则点A，B的对应点A₁，B₁的坐标分别是A₁（________，________），B₁（________，________）．

Answer 1

    0        
分析：作出图形可得△ABO是等腰直角三角形，根据勾股定理求出OA的长度，然后找出旋转后点A₁，B₁的位置，根据平面直角坐标系即可写出点A₁的坐标，过点B₁作B₁C⊥x轴于点C，根据等腰直角三角形的性质求出OC、B₁C的长度，即可得到点B₁的坐标．
解答：解：如图所示，△A₁B₁O为△ABO绕O按顺时针方向旋转135°得到的三角形，
根据勾股定理，OA==2，
∴OA₁=2，
点A₁的坐标为（2，0），
由图可知，△ABO是等腰直角三角形，
过点B₁作B₁C⊥x轴于点C，则OC=B₁C=OA₁=OA=，
所以，点B₁的坐标为（，）．
故答案为：2，0；，．
点评：本题考查了旋转变换与坐标与图形的变化，勾股定理，等腰直角三角形的旋转，根据题意建立平面直角坐标系并画出图形是解题的关键．