题目内容
 如图所示,AB∥CD,AD∥BC,BE=DF,则图中全等三角形共有
如图所示,AB∥CD,AD∥BC,BE=DF,则图中全等三角形共有
- A.2对
- B.3对
- C.4对
- D.5对
B
分析:先证明四边形ABCD是平行四边形,根据平行四边形的对角线把平行四边形分成两个全等的三角形,再利用BE=DF可以证明△ABE≌△CDF,同理可证△AED≌△CFB.
解答:①∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴ABD≌△CDB;
②∵AB∥CD,
∴∠ABD=∠CDB,
在△ABE和△CDF中, ,
,
∴△ABE≌△CDF(ASA);
③∵BE=DF,
∴BE+EF=DF+EF,
即BF=DE,
同理可证△AED≌△CFB;
所以图中全等三角形共有3对.
故选B.
点评:本题主要考查全等三角形的判定,先根据平行证明四边形为平行四边形,再利用平行四边形的性质是解答本题的前提,也是解答本题的突破口和关键.做题时从已知开始结合全等的判定方法由易到难逐个找寻.
分析:先证明四边形ABCD是平行四边形,根据平行四边形的对角线把平行四边形分成两个全等的三角形,再利用BE=DF可以证明△ABE≌△CDF,同理可证△AED≌△CFB.
解答:①∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴ABD≌△CDB;
②∵AB∥CD,
∴∠ABD=∠CDB,
在△ABE和△CDF中,
 ,
,∴△ABE≌△CDF(ASA);
③∵BE=DF,
∴BE+EF=DF+EF,
即BF=DE,
同理可证△AED≌△CFB;
所以图中全等三角形共有3对.
故选B.
点评:本题主要考查全等三角形的判定,先根据平行证明四边形为平行四边形,再利用平行四边形的性质是解答本题的前提,也是解答本题的突破口和关键.做题时从已知开始结合全等的判定方法由易到难逐个找寻.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 5、如图所示,AB∥CD,则∠1+∠2+∠3=( )
5、如图所示,AB∥CD,则∠1+∠2+∠3=( )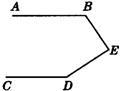 24、已知:如图所示,AB∥CD,若∠ABE=130°,∠CDE=152°,则∠BED=
24、已知:如图所示,AB∥CD,若∠ABE=130°,∠CDE=152°,则∠BED=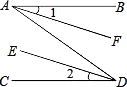 如图所示,AB∥CD,需增加什么条件才能使∠1=∠2成立?
如图所示,AB∥CD,需增加什么条件才能使∠1=∠2成立?
 如图所示,AB∥CD,EG⊥AB,垂足为G,若∠1=42°,则∠E=
如图所示,AB∥CD,EG⊥AB,垂足为G,若∠1=42°,则∠E=