Question

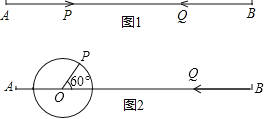
【题目】如图，已知AC、BD为数值的墙面，一架梯子从点O竖起，当靠在墙面AC上时，梯子的另一端落在点A处，此时∠AOC=60°，当靠在墙面BD上时，梯子的另一端落在点B处，此时∠BOD=45°，且OD=3米．

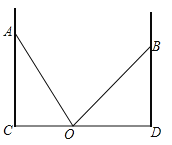
（1）求梯子的长；（2）求OC、AC的长．

Answer 1

【答案】（1）梯子的长为6米；（2）OC=3米；AC=米.

【解析】

（1）先根据题意得出△BOD是等腰直角三角形，再由勾股定理即可得出OB的长；
（2）先根据直角三角形的性质求出OC的长，再由勾股定理即可得出AC的长．

解：（1）∵由题意得，∠BDO=90°，∠BOD=45°，
∴∠B=45°．
∴OD=BD=3（米）．
在Rt△OBD中，=6（米），
∴梯子的长是6米；

（2）∵∠ACO=90°，∠AOC=60°，

∴∠CAO=30°，

∵OA=OB=6米，
∴OC=AO=3米．
在R△ACO中，==米．