题目内容
设x为整数,给出一个流程图如下,按此流程图计算,刚好处理3次,用3与x+2的平均值代替y,则输入的x值是
分析:利用第一次输入时x1=x,y=
>x;则进行第二次输入用x+1代替x,即x2=x+1,则y=
>x+1;则进行第三次输入用x2+1代替x2,即x3=x+1+1=x+2,则第三次输出结束即y=
=x+2,求解即可.
| 3+x+2 |
| 2 |
| 3+x+1+2 |
| 2 |
| 3+x+2+2 |
| 2 |
解答:解:根据题意刚好处理3次,设输入时x1=x,y=
>x;
则进行第二次输入用x+1代替x,即x2=x+1,则y=
>x+1;
则进行第三次输入用x2+1代替x2,即x3=x+1+1=x+2,则第三次输出结束即y=
=x+2①.
由等式方程①解得x=3.
故输入的x的值为3.
| 3+x+2 |
| 2 |
则进行第二次输入用x+1代替x,即x2=x+1,则y=
| 3+x+1+2 |
| 2 |
则进行第三次输入用x2+1代替x2,即x3=x+1+1=x+2,则第三次输出结束即y=
| 3+x+2+2 |
| 2 |
由等式方程①解得x=3.
故输入的x的值为3.
点评:本题考查了有理数的运算.正确理解图示程序及列出代数式是正确解题的关键.

练习册系列答案
相关题目
某公司生产的一种时令商品每件成本为20元,经过市场调研发现,这种商品在未来20天内的日销售量m(件)与时间t(天)的关系如下表:
未来20天内每天的价格y(元/件)与时间t(天)的函数关系式为y =
t+25(1≤t≤20且t为整数).下面我们就来研究销售这种商品的有关问题:
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的关系式;
(2)设未来20天日销售利润为p (元),请写出p (元) 与t(天)之间的关系式;并预测未来20天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)若该公司预计日销售利润不低于560元,请借助(2)小题中的函数图象确定时间的取值范围,持续了多少天?
(4)在实际销售的20天中,该公司决定每销售一件商品就捐赠a元利润(a<5)给希望工程.公司通过销售记录发现,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
| 时间t(天) | 1 | 3 | 6 | 10 | 36 | … |
| 日销售量m(件) | 94 | 90 | 84 | 76 | 24 | … |
| 1 |
| 4 |
(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的关系式;
(2)设未来20天日销售利润为p (元),请写出p (元) 与t(天)之间的关系式;并预测未来20天中哪一天的日销售利润最大,最大日销售利润是多少?
(3)若该公司预计日销售利润不低于560元,请借助(2)小题中的函数图象确定时间的取值范围,持续了多少天?
(4)在实际销售的20天中,该公司决定每销售一件商品就捐赠a元利润(a<5)给希望工程.公司通过销售记录发现,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
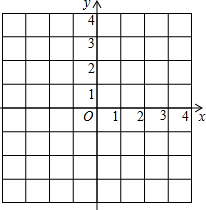 如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现:
如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现:
