题目内容
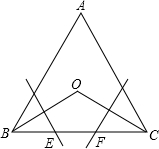
如图，点B、C、E在一条直线上，△ABC、△DCE均为等边三角形，
求证：（1）BD=AE；
（2）△CFG为等边三角形．
求证：（1）BD=AE；
（2）△CFG为等边三角形．
证明：（1）∵△ABC、△DCE均为等边三角形，
∴BC=AC，CD=CE，∠BCA=∠DCE=60°，
∴∠BCA+∠ACD=∠DCE+∠ACD，即∠BCD=∠ACE，
∴△BCD≌△ACE（SAS），
∴BD=AE（全等三角形的对应边相等）；
（2）由（1）知，△BCD≌△ACE，则∠BDC=∠AEC（全等三角形的对应角相等），即∠FDC=∠GEC；
∵△ABC、△DCE均为等边三角形，
∴∠ACB=∠DCE=60°，DC=CE，
∴∠FCG=180°-∠ACB-∠DCE=60°，
∴在△FCD和△GCE中，
，
∴△FCD≌△GCE（ASA），
∴FC=GC（全等三角形的对应边相等），
∴△FCG为等边三角形．
∴BC=AC，CD=CE，∠BCA=∠DCE=60°，
∴∠BCA+∠ACD=∠DCE+∠ACD，即∠BCD=∠ACE，
∴△BCD≌△ACE（SAS），
∴BD=AE（全等三角形的对应边相等）；
（2）由（1）知，△BCD≌△ACE，则∠BDC=∠AEC（全等三角形的对应角相等），即∠FDC=∠GEC；
∵△ABC、△DCE均为等边三角形，
∴∠ACB=∠DCE=60°，DC=CE，
∴∠FCG=180°-∠ACB-∠DCE=60°，
∴在△FCD和△GCE中，
|
∴△FCD≌△GCE（ASA），
∴FC=GC（全等三角形的对应边相等），
∴△FCG为等边三角形．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
