题目内容

如图，以菱形ABCD的两条对角线所在直线为坐标轴建立平面直角坐标系，已知菱形周长为12，∠ABC=120°，则点A的坐标是
（
3
3
2
，0）
（
3
3
2
，0）
．
分析：根据菱形的周长求出边长，再根据菱形的对角线平分一组对角可得∠ABO=60°，然后利用∠ABO的正弦值列式求出OA的长度，即可得解．
解答：解：∵菱形周长为12，
∴菱形边长AB=12÷4=3，
∵∠ABC=120°，
∴∠ABO=
1
2
×120°=60°，
∴OA=AB•sin∠ABO=3×sin60°=3×
3
2
=
3
3
2
，
∴点A的坐标为（
3
3
2
，0）．
故答案为：（
3
3
2
，0）．
点评：本题主要考查了菱形的性质，坐标与图形的性质，利用菱形的对角线平分一组对角求出∠ABO=60°是解题的关键．
练习册系列答案
相关题目
精英家教网如图，以菱形ABCD各边的中点为顶点作四边形A1B1C1D1，再以A1B1C1D1各边的中点为顶点作四边形A2B2C2D2，…，如此下去，得到四边形A2011B2011C2011D2011，若ABCD对角线长分别为a和b，请用含a、b的代数式表示四边形A2011B2011C2011D2011的周长
 
．
精英家教网如图，以菱形ABCD的边AB为直径的⊙O交对角线AC于点P，过P作PE⊥BC，垂足为E．
（1）求证：PE是⊙O的切线；
（2）若菱形ABCD的面积为24，tan∠PAB=
34
，求PE的长．
精英家教网如图，以菱形ABCD两条对角线所在直线建立直角坐标系，对角线交点O为原点，菱形的边长为5，A（-3，0），则B的坐标是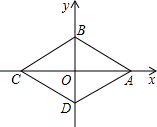
 
．
如图，以菱形ABCD的两条对角线所在直线为坐标轴建立平面直角坐标系，已知菱形周长为12，∠ABC=120°，则点A的坐标是
（
3
3
2
，0）
（
3
3
2
，0）
，若将此菱形绕点O顺时针旋转90°，此时点A的坐标是
（0，-
3
3
2
）
（0，-
3
3
2
）
．
如图，以菱形ABCD的对称中心为坐标原点建立平面直角坐标系，A点坐标为（-4，3）且AD与x轴平行，求其他各点的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网