Question

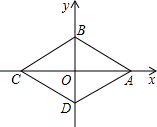如图，以菱形ABCD的两条对角线所在直线为坐标轴建立平面直角坐标系，已知菱形周长为12，∠ABC=120°，则点A的坐标是

（

3 3

2

，0）

，若将此菱形绕点O顺时针旋转90°，此时点A的坐标是

（0，-

3 3

2

）

．

Answer 1

分析：根据菱形的周长求出菱形的边长AB=3，再根据菱形的对角线互相平分求出∠ABO=60°，然后利用∠ABO的正弦值求出OA的长度，从而得到点A的坐标；根据旋转变换的性质可得旋转后点A位于y轴的负半轴，然后根据直角坐标系的特点写出即可．

解答：解：∵菱形周长为12，
∴菱形的边长AB=12÷4=3，
∵∠ABC=120°，
∴∠ABO=

1

2

×120°=60°，
∴OA=AB•sin∠ABO=3•sin60°=3×

3

2

=

3 3

2

，
∴点A的坐标是（

3 3

2

，0），
将此菱形绕点O顺时针旋转90°，点A位于y轴的负半轴，
所以，此时点A的坐标为（0，-

3 3

2

）．
故答案为：（

3 3

2

，0），（0，-

3 3

2

）．

点评：本题考查了坐标与图形的变化，菱形的对角线平分一组对角的性质，熟记性质并求出OA的长度是解题的关键，确定旋转后点A的位置也很重要．