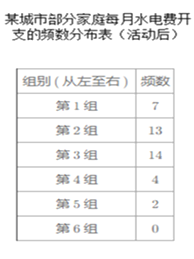
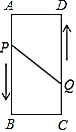
题目内容
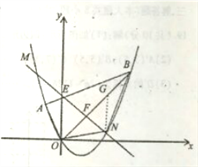
【题目】(12分)如图,平面直角坐标系![]() 中点
中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线经过
,抛物线经过![]() 、
、![]() 、
、![]() 三点,连接
三点,连接![]() ,线段
,线段![]() 交
交![]() 轴于点
轴于点![]() .
.
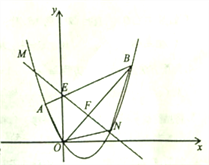
(1)求点![]() 的坐标;
的坐标;
(2)求抛物线的函数解析式;
(3)点![]() 为线段
为线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合),直线
重合),直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点(点
两点(点![]() 在
在![]() 轴右侧),连接
轴右侧),连接![]() ,当四边形
,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标并求出四边形
的坐标并求出四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2) ![]() ;(3) 最大值为
;(3) 最大值为![]() ,此时
,此时![]() 点坐标为
点坐标为![]()
【解析】试题分析:(1)先利用待定系数法求出直线![]() 的解析式,然后计算自变量为0时的函数值即可得到
的解析式,然后计算自变量为0时的函数值即可得到![]() 点坐标;
点坐标;
(2)利用待定系数求抛物线的解析式;
(3)如图1,作![]() 轴交
轴交![]() 于 G,如图,利用一次函数和二次函数图象上点的坐标特征,设设
于 G,如图,利用一次函数和二次函数图象上点的坐标特征,设设![]() ,则
,则![]() ,再根据三角形面积公式计算出
,再根据三角形面积公式计算出
![]() 和
和![]() 然后得到S四边形ABNO和m的二次函数关系式,再根据二次函数的性质求解;
然后得到S四边形ABNO和m的二次函数关系式,再根据二次函数的性质求解;
试题解析:(1)设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入得
代入得![]() ,解得
,解得 ,
,
所以直线![]() 的解析式为
的解析式为![]() ,
,
当![]() 时,
时, ![]() ,
,
所以![]() 点坐标为
点坐标为![]() ;
;
(2)设抛物线解析式为![]() ,
,
把![]() 代入得
代入得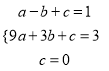 ,解得
,解得 ,
,
所以抛物线解析式为![]() ;
;
(3)如图1,作![]() 轴交
轴交![]() 的解析式为
的解析式为![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]()
所以![]()
当![]() 时,四边形
时,四边形![]() 面积的最大值,最大值为
面积的最大值,最大值为![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ;
;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目