题目内容
阅读下列解题过程:
=
=
=
=
;请回答下列问题:
(1)观察上面的解题过程,化简:①
②
(2)利用上面提供的解法,请计算:(
+
+
+…+
)(
+
).
| 1 | ||||
|
1×(
| ||||||||
(
|
| ||||
(
|
| ||||
| 5-3 |
| ||||
| 2 |
(1)观察上面的解题过程,化简:①
| 4 | ||
|
| 1 | ||||
|
(2)利用上面提供的解法,请计算:(
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 3n+2 |
| 2 |
考点:分母有理化
专题:阅读型
分析:(1)观察阅读材料的解题过程,实质是二次根式的分母有理化,因此解答(1)题的关键是找出分母的有理化因式.
(2)先将第一个括号内的各式分母有理化,此时发现除第一项和最后一项外,每两项都互为相反数,由此可求出第一个括号内各式的和,再求和第二个括号的乘积即可.
(2)先将第一个括号内的各式分母有理化,此时发现除第一项和最后一项外,每两项都互为相反数,由此可求出第一个括号内各式的和,再求和第二个括号的乘积即可.
解答:解:(1)①
=
=
+3;
②
=
=
;
(2)(
+
+
+…+
)(
+
)
=
(
-
+
-
+
-
+…+
-
)(
+
)
=
(
-
)(
+
)
=n.
| 4 | ||
|
4(
| ||||
(
|
| 13 |
②
| 1 | ||||
|
| ||||||||
(
|
| ||||
| 2 |
(2)(
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 3n+2 |
| 2 |
=
| 1 |
| 3 |
| 5 |
| 2 |
| 8 |
| 5 |
| 11 |
| 8 |
| 3n+2 |
| 3n-1 |
| 3n+2 |
| 2 |
=
| 1 |
| 3 |
| 3n+2 |
| 2 |
| 3n+2 |
| 2 |
=n.
点评:此题考查的是二次根式的分母有理化以及二次根式的加减法,关键是寻找分母有理化后的抵消规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知线段AB=4,点P是它的黄金分割点,AP>PB,则PB=( )
A、
| ||||
B、
| ||||
C、2
| ||||
D、6-2
|
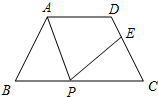 如图,在等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P为BC边上一点(不与B、C重合).过点P作∠APE=∠B,PE交CD于E.
如图,在等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P为BC边上一点(不与B、C重合).过点P作∠APE=∠B,PE交CD于E.