题目内容
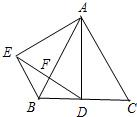7、如图：△ABC为等边三角形，AD平分∠BAC，△ADE是等边三角形，下列结论中：①AD⊥BC ②EF=FD ③BE=BD ④∠ABE=60°中正确的个数为（ ）分析：对等边三角形性质的考查，题中AD为∠BAC的平分线，因为△ABC为等边三角形，所以AD同时也是垂线和中线，然后利用等边三角形的性质及角之间的关系即可判断．
解答：解：∵△ABC为等边三角形，AD平分∠BAC，∴AD⊥BC，BD=DC，∴①正确，
∠BAD=30°，△ADE是等边三角形，∴AF⊥ED，EF=FD，②正确，
由②得AF⊥ED，∴BE=BD，③也正确，
在Rt△BEF中，∠ABE=90°-∠BAE=90°-30°=60°∴④也正确，
∵①②③④都正确，故选A．
∠BAD=30°，△ADE是等边三角形，∴AF⊥ED，EF=FD，②正确，
由②得AF⊥ED，∴BE=BD，③也正确，
在Rt△BEF中，∠ABE=90°-∠BAE=90°-30°=60°∴④也正确，
∵①②③④都正确，故选A．
点评：本题主要考查等边三角形的性质，三边相等、三个角都相等、三线合一．
练习册系列答案
相关题目
16、如图，△ABC为等边三角形，P为三角形内一点，将△ABP绕A点逆时针旋转60°后与△ACP′重合，若AP=3，则PP′=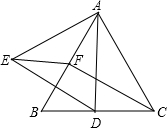
如图，△ABC为等边三角形，D、F分别为BC、AB上的点，且CD=BF，以AD为边作等边△ADE．
如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P，BQ⊥AD与Q，PQ=4，PE=1
如图，△ABC为等边三角形，D、F分别为CB、BA上的点，且CD=BF，以AD为一边作等边三角形ADE．
如图，△ABC为等边△，EC=ED，∠CED=120゜，P为BD的中点，求证：AE=2PE．