题目内容
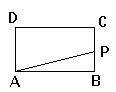
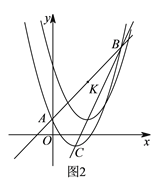
【题目】如图![]() ,二次函数
,二次函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() ,
, ![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第一象限内,点
在第一象限内,点![]() 是二次函数图象的顶点,点
是二次函数图象的顶点,点![]() 是一次函数
是一次函数![]() 的图象与
的图象与![]() 轴的交点,过点
轴的交点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,且
,且![]() .
.
(![]() )求直线
)求直线![]() 和直线
和直线![]() 的解析式.
的解析式.
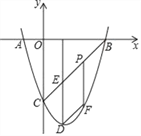
(2)点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 是线段
是线段![]() 上一点,
上一点, ![]() 轴,射线
轴,射线![]() 与抛物线交于点
与抛物线交于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
, ![]() 于点
于点![]() ,当
,当![]() 与
与![]() 的乘积最大时,在线段
的乘积最大时,在线段![]() 上找一点
上找一点![]() (不与点
(不与点![]() ,点
,点![]() 重合),使
重合),使![]() 的值最小,求点
的值最小,求点![]() 的坐标和
的坐标和![]() 的最小值.
的最小值.
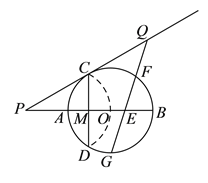
(![]() )如图
)如图![]() ,直线
,直线![]() 上有一点
上有一点![]() ,将二次函数
,将二次函数![]() 沿直线
沿直线![]() 平移,平移的距离是
平移,平移的距离是![]() ,平移后抛物线使点
,平移后抛物线使点![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]() ,点
,点![]() ;当
;当![]() 是直角三角形时,求t的值.
是直角三角形时,求t的值.
【答案】(1)![]() ,
, ![]() ;
;
(2)点![]() ,
, ![]() .
.
(3),t的值为![]() ,
, ![]() 或
或![]() .
.
【解析】试题分析:
试题解析:( ![]() )
)![]() 代入
代入![]() 得
得![]() ,
,
∴一次函数表达式为![]() ,
,
∵![]() ,
,
∴![]()
∵![]() 轴,
轴,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
设![]() 的坐标为
的坐标为![]() ,代入二次函数
,代入二次函数![]() ,
,
解得![]() ,
, ![]() ,
,
∵![]() 在第一象限,
在第一象限,
∴![]() ,点
,点![]() ,
,
∵![]() 是二次函数
是二次函数![]() 的顶点,
的顶点,
∴![]() ,
,
设直线![]() 、
、![]() 解析式分别为
解析式分别为![]() ,
, ![]() ,
,
将![]() ,
, ![]() 代入直线
代入直线![]() 解析式得
解析式得![]() 解得
解得![]() .
.
将![]() ,
, ![]() 代入直线
代入直线![]() 解析式得
解析式得![]() ,解得
,解得![]() .
.
∴![]() ,
, ![]() .
.
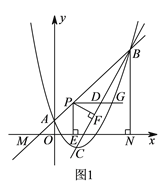
(![]() )如图所示,
)如图所示, ![]() 与
与![]() 交点为
交点为![]() ,
,

过![]() 作
作![]() 轴的平行线
轴的平行线![]() ,
,
过![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,连接
,连接![]() ,
,
设点![]() ,则
,则![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
∵![]() ,
,
![]() 且比值为常数,
且比值为常数,
当![]() 最大时,
最大时, ![]() 的值也最大,
的值也最大,
![]() ,
,
当![]() 时,
时, ![]() 取最大值,
取最大值,
![]() 也最大,此时点
也最大,此时点![]() .
.
代入二次函数得![]() ,
,
得![]() 或
或![]() (舍),
(舍),
∴![]() ,
,
令![]() ,得
,得![]() ,
,
![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,
,
要使![]() 的值最小,即使
的值最小,即使![]() 的值最小,
的值最小,
当![]() 垂直
垂直![]() 时,
时, ![]() 的值最小,
的值最小,
此时![]() ,代入直线
,代入直线![]() 解析式得
解析式得![]() ,
,
∴点![]() ,
,
![]() .
.
(![]() )如图所示,直线
)如图所示,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过
,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,

令![]() ,可求得
,可求得![]() ,
, ![]() 的坐标为
的坐标为![]() .
.
![]() ,
,
 ,
,
设横坐标平移![]() ,纵坐标平移
,纵坐标平移![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
①当![]() 时,
时,
![]() .
.
②当![]() 时,
时,
![]() ,解得
,解得![]() .
.
![]() .
.
③当![]() 时,
时,
![]() ,解得
,解得![]() ,
,
![]() ,
,
综上所述, ![]() 的值为
的值为![]() ,
, ![]() 或
或![]() .
.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】某校篮球队13名同学的身高如下表:
身高(cm) | 175 | 180 | 182 | 185 | 188 |
人数(个) | 1 | 5 | 4 | 2 | 1 |
则该校篮球队13名同学身高的众数和中位数分别是( )
A.182,180
B.180,180
C.180,182
D.188,182