��Ŀ����
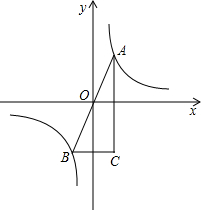
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-2x+2��x�ᡢy��ֱ��ཻ�ڵ�A��B���ı���ABCD�������Σ�����������y=
�ڵ�һ����ͼ����D��
��1����D������꣬�Լ������������Ľ���ʽ��
��2����K��˫�����ϵ�һ�����ڵ�����㣬����AK��BK�����ı���AOBK�����ΪS�����ƶϵ�S�ﵽ���ֵ����Сֵʱ����Ӧ��K������ꣻ��ֱ��д��S��ȡֵ��Χ��
��3����̽������������ABCD�����ң������£�һ��ƽ�����ɸ���λ��C�Ķ�Ӧ��ǡ������˫�����ϵķ�����
| k |
| x |
��1����D������꣬�Լ������������Ľ���ʽ��
��2����K��˫�����ϵ�һ�����ڵ�����㣬����AK��BK�����ı���AOBK�����ΪS�����ƶϵ�S�ﵽ���ֵ����Сֵʱ����Ӧ��K������ꣻ��ֱ��д��S��ȡֵ��Χ��
��3����̽������������ABCD�����ң������£�һ��ƽ�����ɸ���λ��C�Ķ�Ӧ��ǡ������˫�����ϵķ�����

��1����D��DM��OA��M�㣬
������ã�AB=AD����AOB=��AMD��
�֡ߡ�DAM+��BAO=��BAO+��ABO=90�㣬
���ABO=��DAM��
��֤�ã�RT��BAO��RT��ADM����1�֣�
��A��1��0����B��0��2����
��DM=OA=1��AM=OB=2��
��OM=3��D��3��1������1�֣�
��������������ʽΪ��y=
��1�֣�
��2����K�ֱ���KH��BA��H��ֱ��l��AB��
��S�ı���AOBK=S��BOA+S��BKA��S��BOA=1����S��BKA=0.5��
��KH��
��ֱ��lΪ��y=-2x+b��b��2��
��S�ı���AOBK�Ĵ�С���߶�HK�Ĵ�С�йأ���1�֣�
ҪʹHK��С����ֱ��l��˫����y=
�ڵ�һ����ֻ��Ψһ����K��
�ʣ�����-2x+b=
��Ψһʵ����
��2x2-bx+3=0��=b2-24=0��
�֡�b��2����b=2
��
��S��BKA��СʱK������Ϊ��
��
����
�������������ȷ���ɵ�3�֣�
��ֱ��KHΪ��y=
x+
�����ֵã���HK��Сʱ��H�ĺ�����Ϊ��
-
��
��HK��СֵΪ|
-��
-
��|��
=
��
-1����
��S��BKA����СֵΪ
-1��
����֪��HK�����ֵ��
��S�����ֵ���ҵ�K�ĺ�����Ϊ
ʱ��S�ﵽ��Сֵ��
���ԣ�S��ȡֵ��ΧΪ��S��
���������ǹ��̣�S��Χֱ�Ӹ�����ȷ��2�֣�
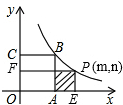
��3����C��CN��BO��N��
�ɵã�CN=BO=2��BN=OA=1��
��C��2��3������1�֣�
�֡ߺ���y=
�У���x=2ʱ��y=1.5����y=3ʱ��x=1����1�֣�
���������ABCD����ƽ��1����λ������ƽ��1.5����λ��
��ʹ��Cǡ���ƶ���˫����y=
�ϣ���1�֣�

������ã�AB=AD����AOB=��AMD��
�֡ߡ�DAM+��BAO=��BAO+��ABO=90�㣬
���ABO=��DAM��
��֤�ã�RT��BAO��RT��ADM����1�֣�
��A��1��0����B��0��2����
��DM=OA=1��AM=OB=2��
��OM=3��D��3��1������1�֣�
��������������ʽΪ��y=
| 3 |
| x |
��2����K�ֱ���KH��BA��H��ֱ��l��AB��
��S�ı���AOBK=S��BOA+S��BKA��S��BOA=1����S��BKA=0.5��
| 5 |
��ֱ��lΪ��y=-2x+b��b��2��
��S�ı���AOBK�Ĵ�С���߶�HK�Ĵ�С�йأ���1�֣�
ҪʹHK��С����ֱ��l��˫����y=
| 3 |
| x |
�ʣ�����-2x+b=
| 3 |
| x |
��2x2-bx+3=0��=b2-24=0��
�֡�b��2����b=2
| 6 |
��S��BKA��СʱK������Ϊ��
| ||
| 2 |
| 6 |
�������������ȷ���ɵ�3�֣�
��ֱ��KHΪ��y=
| 1 |
| 2 |
3
| ||
| 4 |
| 4 |
| 5 |
3
| ||
| 10 |
��HK��СֵΪ|
| ||
| 2 |
| 4 |
| 5 |
3
| ||
| 10 |
| ||
| 2 |
2
| ||
| 5 |
| 6 |
��S��BKA����СֵΪ
| 6 |
����֪��HK�����ֵ��
��S�����ֵ���ҵ�K�ĺ�����Ϊ
| ||
| 2 |
���ԣ�S��ȡֵ��ΧΪ��S��
| 6 |
��3����C��CN��BO��N��
�ɵã�CN=BO=2��BN=OA=1��
��C��2��3������1�֣�
�֡ߺ���y=
| 3 |
| x |
���������ABCD����ƽ��1����λ������ƽ��1.5����λ��
��ʹ��Cǡ���ƶ���˫����y=
| 3 |
| x |

��ϰ��ϵ�д�
�����Ŀ



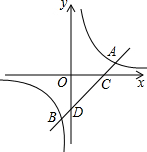 ���ཻ��C��D���㣮
���ཻ��C��D���㣮