题目内容
16.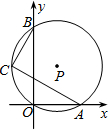 如图,经过原点的⊙P与x轴,y轴分别交于A(3,0),B(0,4)两点,点C是$\widehat{OB}$上一点,且BC=2,则AC=$\sqrt{21}$.
如图,经过原点的⊙P与x轴,y轴分别交于A(3,0),B(0,4)两点,点C是$\widehat{OB}$上一点,且BC=2,则AC=$\sqrt{21}$.
分析 连接AB,根据90度的圆周角所对的弦是直径可以证得AB是直径,利用勾股定理求得直径AB的长,然后在直角△ABC中利用勾股定理求得BC的长.
解答  解:连接AB.
解:连接AB.
∵∠AOB=90°,
∴AB是圆的直径.
∵A的坐标是(3,0),B的坐标是(0,4),
∴OA=3,OB=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵AB是直径,
∴∠C=90°,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{{5}^{2}-{2}^{2}}$=$\sqrt{21}$.
故答案是:$\sqrt{21}$.
点评 本题考查了圆周角定理的推论,注意到AB是圆的直径是解决本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
6.在下列图形中,①等边三角形;②平行四边形;③正方形;④圆.既是轴对称图形又是中心对称图形的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,△ABC是等边三角形,点E是AB的中点,延长CB至D,使BD=$\frac{1}{2}$BC.
如图,△ABC是等边三角形,点E是AB的中点,延长CB至D,使BD=$\frac{1}{2}$BC.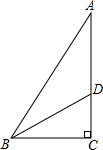 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BC=4cm,BD=5cm,则点D到AB的距离是3cm.
如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BC=4cm,BD=5cm,则点D到AB的距离是3cm.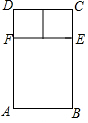 如图是一种窗框的设计示意图,矩形ABCD被分成上下两部分,上部的矩形CDFE由两个正方形组成,制作窗框的材料总长为6m.
如图是一种窗框的设计示意图,矩形ABCD被分成上下两部分,上部的矩形CDFE由两个正方形组成,制作窗框的材料总长为6m.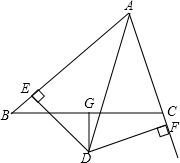 如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F. 如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则矩形ABCD的面积为16$\sqrt{3}$cm2.
如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则矩形ABCD的面积为16$\sqrt{3}$cm2.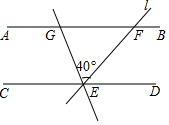 如图,已知直线AB∥CD,直线l与直线AB、CD相交于点,E、F,将l绕点E逆时针旋转40°后,与直线AB相交于点G,若∠GEC=80°,那么∠GFE=( )
如图,已知直线AB∥CD,直线l与直线AB、CD相交于点,E、F,将l绕点E逆时针旋转40°后,与直线AB相交于点G,若∠GEC=80°,那么∠GFE=( )