题目内容
（8分）在圆内接四边形ABCD中，CD为∠BCA外角的平分线，F为弧AD上一点，BC=AF，延长DF与BA的延长线交于E．
⑴求证△ABD为等腰三角形．
⑵求证AC•AF=DF•FE
⑴由圆的性质知∠MCD=∠DAB、∠DCA=∠DBA，而∠MCD=∠DCA，所以∠DBA=∠DAB，故△ABD为等腰三角形．
⑵∵∠DBA=∠DAB
∴弧AD=弧BD
又∵BC=AF
∴弧BC=弧AF、∠CDB=∠FDA
∴弧CD=弧DF
∴CD=DF
再由“圆的内接四边形外角等于它的内对角”知
∠AFE=∠DBA=∠DCA①，∠FAE=∠BDE
∴∠CDA=∠CDB＋∠BDA=∠FDA＋∠BDA=∠BDE=∠FAE② 由①②得△DCA∽△FAE
∴AC：FE=CD：AF
∴AC•AF= CD•FE
而CD=DF，
∴AC•AF=DF•FE解析:
略
⑵∵∠DBA=∠DAB
∴弧AD=弧BD
又∵BC=AF
∴弧BC=弧AF、∠CDB=∠FDA
∴弧CD=弧DF
∴CD=DF
再由“圆的内接四边形外角等于它的内对角”知
∠AFE=∠DBA=∠DCA①，∠FAE=∠BDE
∴∠CDA=∠CDB＋∠BDA=∠FDA＋∠BDA=∠BDE=∠FAE② 由①②得△DCA∽△FAE
∴AC：FE=CD：AF
∴AC•AF= CD•FE
而CD=DF，
∴AC•AF=DF•FE解析:
略
练习册系列答案
相关题目
（2013•梧州一模）如图，在圆的内接四边形ABCD中，∠ABC=120°，则四边形ABCD的外角∠ADE的度数是（ ）
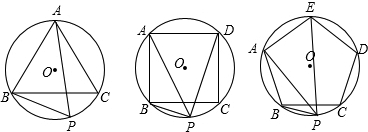
上一点，则PB+PC=PA；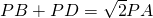
；
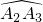上一点，请问PA2+PAn与PA1又有怎样的数量关系，写出结论，不要求证明．
上一点，则PB+PC=PA；
上一点，则
；
上一点，请问PB+PE与PA有怎样的数量关系，写出结论，并加以证明；
上一点，请问PA2+PAn与PA1又有怎样的数量关系，写出结论，不要求证明．
°