题目内容
6.如图1,B,C,E三点在一条直线上,△CAB和△CDE均为等边三角形,连接AE,BD,则有结论:AE=BD.请你完成下面的探究:如果把图1中的△CDE绕点C顺时针旋转一个角度(旋转角小于60°),如图2所示,结论AE=BD还成立吗?请证明你的猜想,并求出AE与BD所夹锐角的度数.

分析 结论还成立.根据等边三角形的各边都相等得:CB=CA,CD=CE,由各角为60°得:∠BCA=∠DCE=60°,由等式的性质得:∠BCD=∠ACE,利用SAS证明△BCD≌△ACE;
在△DFG和△EGC中,根据两个角对应相等,则第三个角相等得:∠DFE=∠DCE=60°,所以,AE与BD所夹锐角的度数为60°.
解答 证明:如图2,结论还成立.
∵△CAB和△CDE均为等边三角形,
∴CB=CA,CD=CE,∠BCA=∠DCE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
$\left\{\begin{array}{l}CB=CA\\∠BCD=∠ACE\\ CD=CE\end{array}\right.$,
∴△BCD≌△ACE(SAS),
∴BD=AE,
∵△BCD≌△ACE,
∴∠BDC=∠AEC,
∵∠DGF=∠EGC,
∴∠DFE=∠DCE=60°,
所以,AE与BD所夹锐角的度数为60°.
点评 本题考查了等边三角形的性质、全等三角形的性质和判定,属于常考题型,解题的关键是能利用等边三角形的性质得到相等的线段和相等的角,从而证得三角形全等,进一步证得结论.

练习册系列答案
相关题目
16.某工厂2015年总产值是a万元,预计2016年总产值比2015年增长20%,则该工厂2016年生产总值是( )
| A. | (a+20%) 万元 | B. | (1+20%)a万元 | C. | $\frac{a}{1-20%}$万元 | D. | $\frac{a}{1+20%}$万元 |
17.为了解太原市迎泽区老年人的健康状况,小颖准备采用抽样调查的方式,调查迎泽区部分老年人一年中生病的次数.下列抽取样本的方式中,最合理的是( )
| A. | 在迎泽公园随机抽取100名老年人调查 | |
| B. | 在迎泽区某医院随机抽取50名老年人调查 | |
| C. | 在小颖家所在小区内,抽取10名老年邻居调查 | |
| D. | 利用迎泽区公安局的户籍网,随机抽取本区10%的老年人调查 |
14.下列计算正确的是( )
| A. | a8÷a2=a6 | B. | (a+1)2=a2+1 | C. | a2+a3=a5 | D. | 3a2-2a2=1 |
11.下列四边形中,是轴对称但不是中心对称的图形是( )
| A. |  | B. |  | C. |  | D. |  |
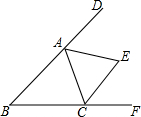 如图,△ABC中,∠B=30°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC的度数为75°.
如图,△ABC中,∠B=30°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC的度数为75°.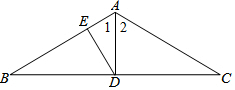 如图,在△ABC中,∠B=∠C=30°,D是BC边上的中点,DE⊥AB于E,BC=12.求:
如图,在△ABC中,∠B=∠C=30°,D是BC边上的中点,DE⊥AB于E,BC=12.求: 如图,在圆O中,弦AB⊥CD于E,弦AG⊥BC于F,CD与AG相交于点M.
如图,在圆O中,弦AB⊥CD于E,弦AG⊥BC于F,CD与AG相交于点M.