题目内容
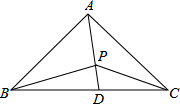 如图,△ABC中,AB=AC,∠BAC=90°,点D在BC上,连接AD,点P在AD上,连接PC、PB.若tan∠CPD=2,PB=
如图,△ABC中,AB=AC,∠BAC=90°,点D在BC上,连接AD,点P在AD上,连接PC、PB.若tan∠CPD=2,PB= ,且△APC与△BPC的面积相等,则AB的长为________.
,且△APC与△BPC的面积相等,则AB的长为________.
2
分析:延长CP,过点A点B分别作AE⊥CE,BF⊥CF,CF交AB于O,过P作PN⊥AB于N,设AB=AC=2a,求出AE=BF,求出AO=BO=a,求出AO=AP=a,求出OE、PE、求出OP、求出ON、PN、求出BN、在Rt△BNP中,根据勾股定理即可求出a.
解答: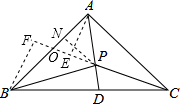
解:延长CP,过点A点B分别作AE⊥CE,BF⊥CF,CF交AB于O,过P作PN⊥AB于N,
设AB=AC=2a,
∵S△APC=S△BPC,
∴CP×AE=CP×BF,
∴AE=BF
∵∠AOE=∠BOF,∠BFO=∠AEO=90°,
∴在△BFO和△AEO中
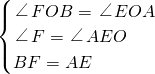
∴△BFO≌△∠AEO,
∴AO=BO=a,
在RT△OAC中,tan∠AOC= =2,
=2,
∵tan∠APO=tan∠CPD=2,
∴tan∠AOP=tan∠APO,
∴∠AOP=∠APO,
∴AP=AO=a,
在Rt△AEO中,tan∠AOP=2=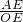 ,
,
∴AE=2OE,
∵AO=a,由勾股定理得:OE2+(2OE)2=a2,
OE= a,
a,
∵AO=AP,AE⊥OP,
∴OE=PE= a,
a,
∴OP= a,
a,
在Rt△OPN中,tan∠AOP=2=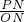 ,
,
∴PN=2ON,
∵OP= a,由勾股定理得:ON2+(2ON)2=(
a,由勾股定理得:ON2+(2ON)2=( a)2,
a)2,
∴ON= a,PN=2ON=
a,PN=2ON= a,BN=a+
a,BN=a+ a=
a= a,
a,
在Rt△PNB中,由勾股定理得:BN2+PN2=BP2,
( a)2+(
a)2+( a)2=(
a)2=( )2,
)2,
a= ,
,
∴AB=2a=2 ,
,
故答案为:2 .
.
点评:本题考查了勾股定理,等腰直角三角形,解直角三角形,全等三角形的性质和判定的应用,综合性比较强,难度偏大.

分析:延长CP,过点A点B分别作AE⊥CE,BF⊥CF,CF交AB于O,过P作PN⊥AB于N,设AB=AC=2a,求出AE=BF,求出AO=BO=a,求出AO=AP=a,求出OE、PE、求出OP、求出ON、PN、求出BN、在Rt△BNP中,根据勾股定理即可求出a.
解答:

解:延长CP,过点A点B分别作AE⊥CE,BF⊥CF,CF交AB于O,过P作PN⊥AB于N,
设AB=AC=2a,
∵S△APC=S△BPC,
∴CP×AE=CP×BF,
∴AE=BF
∵∠AOE=∠BOF,∠BFO=∠AEO=90°,
∴在△BFO和△AEO中
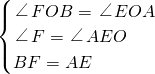
∴△BFO≌△∠AEO,
∴AO=BO=a,
在RT△OAC中,tan∠AOC=
 =2,
=2,∵tan∠APO=tan∠CPD=2,
∴tan∠AOP=tan∠APO,
∴∠AOP=∠APO,
∴AP=AO=a,
在Rt△AEO中,tan∠AOP=2=
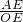 ,
,∴AE=2OE,
∵AO=a,由勾股定理得:OE2+(2OE)2=a2,
OE=
 a,
a,∵AO=AP,AE⊥OP,
∴OE=PE=
 a,
a,∴OP=
 a,
a,在Rt△OPN中,tan∠AOP=2=
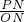 ,
,∴PN=2ON,
∵OP=
 a,由勾股定理得:ON2+(2ON)2=(
a,由勾股定理得:ON2+(2ON)2=( a)2,
a)2,∴ON=
 a,PN=2ON=
a,PN=2ON= a,BN=a+
a,BN=a+ a=
a= a,
a,在Rt△PNB中,由勾股定理得:BN2+PN2=BP2,
(
 a)2+(
a)2+( a)2=(
a)2=( )2,
)2,a=
 ,
,∴AB=2a=2
 ,
,故答案为:2
 .
.点评:本题考查了勾股定理,等腰直角三角形,解直角三角形,全等三角形的性质和判定的应用,综合性比较强,难度偏大.

练习册系列答案
相关题目
 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB. 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( ) 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.