Question

20．如图，每个小正方形边长都是1，以格点为要求画三角形．
（1）使三角形三边长分别为$2\sqrt{2}，\sqrt{13}，\sqrt{17}$；
（2）求该三角形的面积．

Answer 1

分析 （1）由勾股定理得出$2\sqrt{2}，\sqrt{13}，\sqrt{17}$，即可画出图形；
（2）用矩形的面积减去三个直角三角形的面积即可得出所求三角形的面积．

解答 解：（1）由勾股定理得：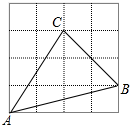
BC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$，AC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$，AB=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$，
△ABC即为所求，如图所示；

（2）△ABC的面积
=4×3-$\frac{1}{2}$×4×1-$\frac{1}{2}$×2×2-$\frac{1}{2}$×2×3
=5．

点评 本题考查了勾股定理、三角形面积的计算方法；熟练掌握勾股定理，根据边长画出三角形是解决问题的关键．