Question

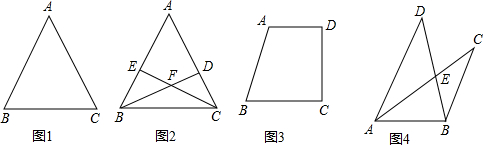
如图1，△ABC是等腰直角三角形，∠BAC=90°，AB=AC，四边形ADEF是正方形，D、F分别在AB、AC边上，此时BD=CF，BD⊥CF成立．

（1）当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由．

（2）当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G．

①求证：BD⊥CF；

②当AB=4，AD=时，求线段FG的长．                                

 

Answer 1

解：（1）BD=CF成立。                     ………………1分

理由如下：

∵△ABC是等腰直角三角形，四边形ADEF是正方形，

∴AB=AC，AD=AF。               ………………2分

∵当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°），

∴∠BAD=∠CAF=θ。             ………………3分

在△BAD和△CAF中，∵AB=AC，∠BAD=∠CAF，AD=AF，

∴△BAD≌△CAF（SAS）       

∴BD=CF。                     ………………4分

（2）①证明：设BG交AC于点M．

∵△BAD≌△CAF（已证），∴∠ABG=∠GCA。  ………………5分

又∵∠BMA=∠CMG，

∴∠BGC=∠BAC=90°。                       ………………6分

∴BG⊥CF，即BD⊥CF。

②解法一：

如图，连接FD，交AC于点N

∵在正方形ADEF中，AD=DE=

∴AN=FN=AE=1，FD=2。

∵在等腰直角△ABC 中，AB=4，∴CN=AC-AN=3，

∴在Rt△FCN中，。………7分

∵△BAD≌△CAF（已证），∴BD=CF=。

设FG=，在Rt△FGD中，∵FD=2，∴GD=。………………8分

∵CF=，∴CG=。

∵在等腰直角△ABC 中，AB=AC=4，，∴。

                                    ………………9分

∵在Rt△BCG中，

∴      …………11分

整理，得

解之，得，（不合题意，故舍去）

∴FG=。                                ………………14分

解法二：

如图，连接FD，交AC于点N；连接CD。     

 ………………7分

同解法一，可得：

DG=，CG=， ………………8分

易证△ACD≌△ABD（SAS），                 ………………9分

可得CD=BD=，                           ………………10分

在Rt△CGD中，

即           ………………12分

解之，得    故FG=