题目内容
已知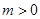 ,点
,点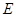 的坐标为
的坐标为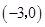 ,关于
,关于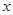 的二次函数
的二次函数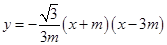 图象的顶点为
图象的顶点为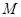 ,图象交
,图象交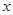 轴于
轴于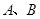 两点,交
两点,交 轴正半轴于
轴正半轴于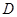 点.以
点.以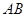 为直径作圆,其圆心为
为直径作圆,其圆心为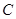 .
. 
(1)写出
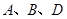 三点的坐标(可用含
三点的坐标(可用含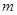 的代数式表示);
的代数式表示);(2)当
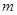 为何值时
为何值时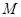 点在直线
点在直线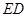 上?判定此时直线
上?判定此时直线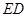 与圆的位置关系?
与圆的位置关系?(3)连接
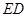 ,当
,当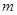 变化时,试用
变化时,试用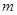 表示
表示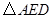 的面积
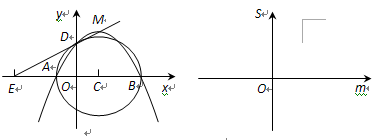
的面积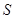 ,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
(1) (2)当
(2)当 时,
时, 点在直线
点在直线 上,直线
上,直线 与
与 相切,(3)
相切,(3) 解析:
解析:
解:(1) …………3分
…………3分
(2)设直线 的解析式为
的解析式为 ,
,
将 代入得:
代入得:
 …………4分
…………4分
解得,
 直线
直线 的解析式为
的解析式为 …………5分
…………5分
将 化为顶点式:
化为顶点式:
 顶点
顶点 的坐标为
的坐标为 …………7分
…………7分
代入 得:
得:

所以,当 时,
时, 点在直线
点在直线 上. …………8分
上. …………8分
连接 为
为 中点,
中点, 点坐标为
点坐标为 .
.
 点在圆上,
点在圆上,
又


 直线
直线 与
与 相切.…………10分
相切.…………10分
(3)当 时,
时,
即: …………11分
…………11分
当 时,
时,
即: …………12分
…………12分
其图象示意图如图中实线部分.
(1)通过二次函数求得 三点的坐标
三点的坐标
(2)通过E、D坐标求得 的解析式,求出
的解析式,求出 的坐标,再利用勾股定理的逆定理求出
的坐标,再利用勾股定理的逆定理求出 从而得出结论
从而得出结论
(3)从当 时,当
时,当 时两种情况进行讨论
时两种情况进行讨论
 (2)当
(2)当 时,
时, 点在直线
点在直线 上,直线
上,直线 与
与 相切,(3)
相切,(3) 解析:
解析:解:(1)
 …………3分
…………3分(2)设直线
 的解析式为
的解析式为 ,
,将
 代入得:
代入得: …………4分
…………4分解得,

 直线
直线 的解析式为
的解析式为 …………5分
…………5分将
 化为顶点式:
化为顶点式:
 顶点
顶点 的坐标为
的坐标为 …………7分
…………7分代入
 得:
得:

所以,当
 时,
时, 点在直线
点在直线 上. …………8分
上. …………8分连接
 为
为 中点,
中点, 点坐标为
点坐标为 .
. 点在圆上,
点在圆上,又



 直线
直线 与
与 相切.…………10分
相切.…………10分(3)当
 时,
时,
即:
 …………11分
…………11分当
 时,
时,
即:
 …………12分
…………12分其图象示意图如图中实线部分.

(1)通过二次函数求得
 三点的坐标
三点的坐标(2)通过E、D坐标求得
 的解析式,求出
的解析式,求出 的坐标,再利用勾股定理的逆定理求出
的坐标,再利用勾股定理的逆定理求出 从而得出结论
从而得出结论(3)从当
 时,当
时,当 时两种情况进行讨论
时两种情况进行讨论 
练习册系列答案
相关题目
 如图,点A是函数y=
如图,点A是函数y=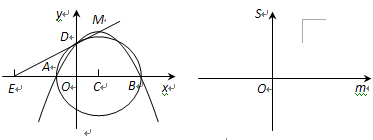
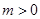 ,点
,点 的坐标为
的坐标为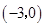 ,关于
,关于 的二次函数
的二次函数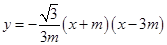 图象的顶点为
图象的顶点为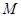 ,图象交
,图象交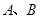 两点,交
两点,交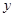 轴正半轴于
轴正半轴于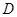 点.以
点.以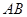 为直径作圆,其圆心为
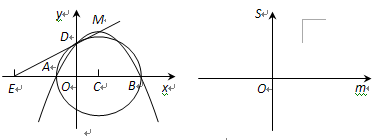
为直径作圆,其圆心为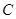 .
. 
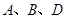 三点的坐标(可用含
三点的坐标(可用含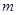 的代数式表示);
的代数式表示);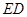 上?判定此时直线
上?判定此时直线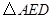 的面积
的面积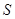 ,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
,并在给出的直角坐标系中画出S关于m的函数图象的示意图.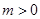 ,点
,点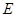 的坐标为
的坐标为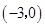 ,关于
,关于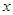 的二次函数
的二次函数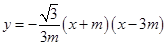 图象的顶点为
图象的顶点为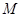 ,图象交
,图象交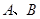 两点,交
两点,交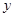 轴正半轴于
轴正半轴于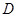 点.以
点.以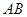 为直径作圆,其圆心为
为直径作圆,其圆心为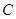 .
.
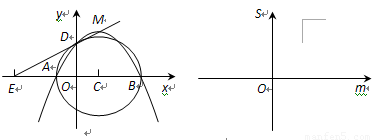
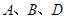 三点的坐标(可用含
三点的坐标(可用含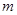 的代数式表示);
的代数式表示);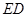 上?判定此时直线
上?判定此时直线 的面积
的面积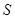 ,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
,并在给出的直角坐标系中画出S关于m的函数图象的示意图.