题目内容
一个正比例函数图象与一次函数y=-x+2的图象交于点P,点P到x轴距离为2,则这个正比例函数的表达式是 .
考点:两条直线相交或平行问题
专题:计算题
分析:由点P到x轴距离为2得到P点的纵坐标为2或-2,再利用点P在直线y=-x+2确定P点坐标(其中点P在y轴上不合题意舍去),然后利用待定系数法求正比例函数解析式.
解答:解:∵点P到x轴距离为2,
∴P点的纵坐标为2或-2,
当y=2时,-x+2=2,解得x=0,不合题意舍去;
当y=-2时,-x+2=-2,解得x=4,此时P点坐标为(4,-2),
设正比例函数解析式为y=kx,
把P(4,-2)代入得4k=-2,解得k=-
,
∴正比例函数的解析式为y=-
x.
故答案为y=-
x.
∴P点的纵坐标为2或-2,
当y=2时,-x+2=2,解得x=0,不合题意舍去;
当y=-2时,-x+2=-2,解得x=4,此时P点坐标为(4,-2),
设正比例函数解析式为y=kx,
把P(4,-2)代入得4k=-2,解得k=-
| 1 |
| 2 |
∴正比例函数的解析式为y=-
| 1 |
| 2 |
故答案为y=-
| 1 |
| 2 |
点评:本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
相关题目
经过调查研究,某工厂生产一种产品的总利润L(元)与产量x(件)的关系式为L=-x2+2000x-10000(0<x<1900),要使总利润达到99万元,则这种产品应生产( )
| A、1000件 |
| B、1200件 |
| C、2000件 |
| D、10000件 |
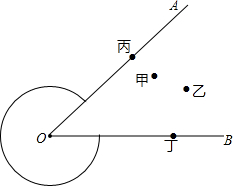 甲乙丙丁四位同学在铅球场地做接力游戏,其中丙在OA边,丁在OB边.游戏规则是,甲将接力棒传给丙,丙传给丁,丁传给乙,乙最后丁跑回甲处.那么丙丁两人站在何处,才能使四人的路程和最短?(请画出路线,并保留作图痕迹,作法不用写)
甲乙丙丁四位同学在铅球场地做接力游戏,其中丙在OA边,丁在OB边.游戏规则是,甲将接力棒传给丙,丙传给丁,丁传给乙,乙最后丁跑回甲处.那么丙丁两人站在何处,才能使四人的路程和最短?(请画出路线,并保留作图痕迹,作法不用写) 如图,是一个圆锥形粮仓顶盖,底面半径为5m,圆锥的高为5
如图,是一个圆锥形粮仓顶盖,底面半径为5m,圆锥的高为5 如图,已知△ABC中,∠B=∠C,BD=5cm,BC=8cm.如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段AC上由C点向A点运动.
如图,已知△ABC中,∠B=∠C,BD=5cm,BC=8cm.如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段AC上由C点向A点运动.