题目内容
 如图,ABCD是一矩形纸片,E是AB上的一点,且BE:EA=5:3,EC=15
如图,ABCD是一矩形纸片,E是AB上的一点,且BE:EA=5:3,EC=15| 5 |
y=-
x+16
| 4 |
| 3 |
y=-
x+16
.| 4 |
| 3 |
分析:设BE=5x,AE=3x,根据矩形ABCD,得到∠DAB=∠B=∠CDA=90°,CD=8x,由勾股定理求出AF=4x,根据翻折,求出EF=BE=5x,∠ABC=∠EFC=90°,推出∠AFE=∠DCF,证△AFE∽△DCF,得到
=
,求出DF=6x,BC=10x,由勾股定理得出EC2=BE2+BC2,求出x=3,得到F(12,0),C(30,-24),设直线CF的解析式是y=kx+b,代入得到方程组
,求出方程组的解饥渴.
| AF |
| DC |
| AE |
| DF |
|
解答:解:设BE=5x,AE=3x,
∵矩形ABCD,
∴∠DAB=∠B=∠CDA=90°,CD=8x,
由勾股定理得:AF=
=4x,
∵△BCE沿折痕EC向上翻折,若点B恰好落在AD边F上,
∴EF=BE=5x,∠ABC=∠EFC=90°,
∴∠AFE+∠DFC=90°,∠DFC+∠DCF=90°,
∴∠AFE=∠DCF,
∴△AFE∽△DCF,
∴
=
,
∴
=
,
∴DF=6x,
BC=AD=6x+4x=10x,
由勾股定理得:EC2=BE2+BC2,
(5x)2+(10x)2=(15
)2,
x=3,8x=24,4x=12,10x=30,
∴F(12,0),C(30,-24),
设直线CF的解析式是y=kx+b,代入得:
,
∴
,
∴y=-
x+16.
故答案为:y=-
x+16.
∵矩形ABCD,
∴∠DAB=∠B=∠CDA=90°,CD=8x,
由勾股定理得:AF=
| EF2-AE2 |
∵△BCE沿折痕EC向上翻折,若点B恰好落在AD边F上,
∴EF=BE=5x,∠ABC=∠EFC=90°,
∴∠AFE+∠DFC=90°,∠DFC+∠DCF=90°,
∴∠AFE=∠DCF,
∴△AFE∽△DCF,
∴
| AF |
| DC |
| AE |
| DF |
∴
| 4x |
| 8x |
| 3x |
| DF |
∴DF=6x,
BC=AD=6x+4x=10x,
由勾股定理得:EC2=BE2+BC2,
(5x)2+(10x)2=(15
| 5 |
x=3,8x=24,4x=12,10x=30,
∴F(12,0),C(30,-24),
设直线CF的解析式是y=kx+b,代入得:
|
∴
|
∴y=-
| 4 |
| 3 |
故答案为:y=-
| 4 |
| 3 |
点评:本题主要考查对一次函数的综合题,翻折变换,矩形的性质,勾股定理,解二元一次方程组,解一元一次方程,用待定系数法求一次函数的解析式等知识点的理解和掌握,综合运用性质进行推理是解此题的关键.

练习册系列答案
相关题目
 B、
B、 C、
C、 D、
D、

 如图,ABCD是一矩形纸片,E是AB上的一点,且BE:EA=5:3,EC=
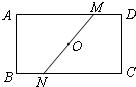
如图,ABCD是一矩形纸片,E是AB上的一点,且BE:EA=5:3,EC= ,把△BCE沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点是F,以点A为原点,以直线AD为x轴,以直线BA为y轴,则过点F、点C的一次函数解析式为:________.
,把△BCE沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点是F,以点A为原点,以直线AD为x轴,以直线BA为y轴,则过点F、点C的一次函数解析式为:________. ,把△BCE沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点是F,以点A为原点,以直线AD为x轴,以直线BA为y轴,则过点F、点C的一次函数解析式为: .
,把△BCE沿折痕EC向上翻折,若点B恰好落在AD边上,设这个点是F,以点A为原点,以直线AD为x轴,以直线BA为y轴,则过点F、点C的一次函数解析式为: .