题目内容
【题目】如图,AB是⊙O的弦,OC⊥AB于点C,连接OA,AB=12,⊙O半径为10.

(1)求OC的长;
(2)点E,F在⊙O上,EF∥AB.若EF=16,直接写出EF与AB之间的距离.
【答案】(1)8; (2)2或14.
【解析】
试题分析:(1)由垂径定理求得AC=6;然后通过解Rt△AOC来求OC的长度;
(2)需要分类讨论:EF在圆心是下方和EF在圆心的上方两种情况.
试题解析:(1)∵AB是⊙O的弦,OC⊥AB于C,AB=12,
∴AC=![]() AB=6.
AB=6.
∵在Rt△AOC中,∠ACO=90°,cosA=![]() ,
,
∴OA=10,
∴OC=![]() =8;
=8;
(2)设直线CO交EF于点D,连接OE.
∵EF∥AB,
∴OD⊥EF,ED=![]() EF=8.
EF=8.
∴在直角△OED中,根据勾股定理得到:OD=![]()
如图1,CD=OC-OD=8-6=2;
如图2,CD=OC,+OD=8+6=14;
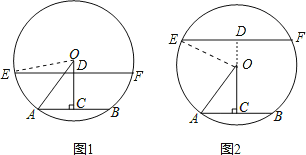
综上所述,EF与AB之间的距离是2或14.

练习册系列答案
相关题目