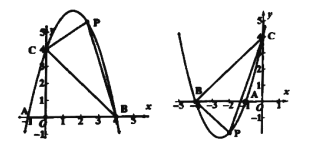题目内容
【题目】如图,在平面直角坐标系xOy中,函数![]() (
(![]() )的图象经过点
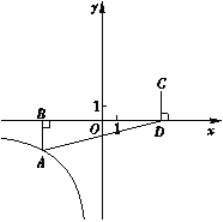
)的图象经过点![]() ,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
(1)求m,n的值;
(2)若直线![]() (k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当
(k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当![]() 时,求点F的坐标.
时,求点F的坐标.
【答案】(1)m=8,n=-2;(2) 点F的坐标为![]() ,
,![]()
【解析】(1)利用三角形的面积公式构建方程求出n,再利用 待定系数法求出m的的值即可;(2)分两种情形分别求解如①图,当k<0时,设直线y=kx+b与x轴,y轴的交点分别为![]() ,
,![]() . ②图中,当k>0时,设直线y=kx+b与x轴,y轴的交点分别为点
. ②图中,当k>0时,设直线y=kx+b与x轴,y轴的交点分别为点![]() ,
,![]() .
.
(1)如图②

∵ 点A的坐标为![]() ,点C与点A关于原点O对称,
,点C与点A关于原点O对称,
∴ 点C的坐标为![]() .
.
∵ AB⊥x轴于点B,CD⊥x轴于点D,
∴ B,D两点的坐标分别为![]() ,
,![]() .
.
∵ △ABD的面积为8,![]() ,
,
∴ ![]() .
.
解得 ![]() . ∵ 函数
. ∵ 函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,
,
∴ ![]() .
.
(2)由(1)得点C的坐标为![]() .
.
① 如图,当![]() 时,设直线
时,设直线![]() 与x轴,
与x轴,
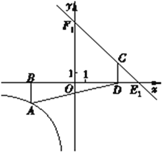
y轴的交点分别为点![]() ,
,![]() .
.
由 CD⊥x轴于点D可得CD∥![]() .
.
∴ △![]() CD∽△
CD∽△![]()
![]() O.
O.
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
∴ 点![]() 的坐标为
的坐标为![]() .
.
②如图,当![]() 时,设直线
时,设直线![]() 与x轴,y轴的交点分别为
与x轴,y轴的交点分别为
点![]() ,
,![]() .
.
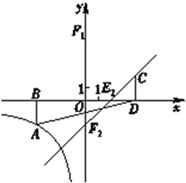
同理可得CD∥![]() ,
,![]() .
.
∵ ![]() ,
,
∴ ![]() 为线段
为线段![]() 的中点,
的中点,![]() .
.
∴ ![]() .
.
∴ 点![]() 的坐标为
的坐标为![]() .
.
综上所述,点F的坐标为![]() ,
,![]() .
.

练习册系列答案
相关题目