Question

【题目】如图，已知长方形ABCD中，AD＝6cm，AB＝4cm，点E为AD的中点．若点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BC上由点B向点C运动．

(1)若点Q的运动速度与点P的运动速度相等，经过1秒后，△AEP与△BPQ是否全等，请说明理由，并判断此时线段PE和线段PQ的位置关系；

(2)若点Q的运动速度与点P的运动速度相等，运动时间为t秒，设△PEQ的面积为Scm2，请用t的代数式表示S；

(3)若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△AEP与△BPQ全等？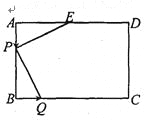

Answer 1

【答案】（1）见详解；（2）S=t+6；（3）

【解析】

（1）本题很容易证明△AEP≌△BPQ，这样可得出∠AEP=∠BPQ，因为∠AEP+∠APE=90°，可得出∠BPQ+∠APE=90°，这即可判断出结论．
（2）可分别用t表示出AP、BQ、BP、CQ的长度，然后用矩形的面积减去△APE、△BPQ及梯形EDCQ的面积即可得出△PEQ的面积为Scm2．
（3）设Q运动的速度为xcm/s，则根据△AEP与△BQP得出AP=BP、AE=BQ或AP=BQ，AE=BP，从而可列出方程组，解出即可得出答案．

(1)∵长方形ABCD，

∴∠A=∠B=90°，

∵点E为AD的中点，AD=6cm，

∴AE=3cm，

又∵P和Q的速度相等可得出AP=BQ=1cm，BP=3，

∴AE=BP，

在△AEP和△BQP中，

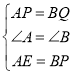
∴△AEP≌△BPQ，

∴∠AEP=∠BPQ，

又∵∠AEP+∠APE=90°，

故可得出∠BPQ+∠APE=90°,即∠EPQ=90°，

即EP⊥PQ.

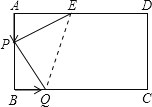
(2)连接QE,由题意得：AP=BQ=t,BP=4t,CQ=6t,

SPEQ=SABCDSBPQSEDCQSAPE

=AD×ABAE×APBP×BQ (DE+CQ)×CD

=24×3tt(4t) ×4(3+6t)

=t+6，

(3)设点Q的运动速度为xcm/s，

①经过y秒后,△AEP≌△BQP，则AP=BP，AE=BQ，

∴，

解得：，

即点Q的运动速度为cm/s时能使两三角形全等.

②经过y秒后,△AEP≌△BPQ，则AP=BQ，AE=BP，

∴

解得： (舍去).

综上所述,点Q的运动速度为cm/s时能使两三角形全等.