题目内容
已知直线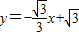 交x轴于点A,交y轴于点C,点B在坐标轴上,△ABC为等腰三角形,且底角等于30°,则点B的坐标为 .
交x轴于点A,交y轴于点C,点B在坐标轴上,△ABC为等腰三角形,且底角等于30°,则点B的坐标为 .
【答案】分析:先根据题意画出图形,利用特殊角的三角函数值求出∠CAO的度数,在分当点B在x轴上与点B在y轴上两种情况进行解答即可.
解答: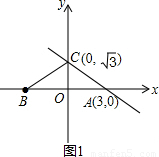 解:∵直线
解:∵直线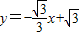 交x轴于点A,交y轴于点C,
交x轴于点A,交y轴于点C,
∴A(3,0),B(0,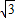 ),
),
∵OC=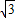 ,OA=3,
,OA=3,
∴tan∠CAO=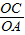 =
=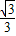 ,
,
∴∠CAO=30°,
当点B在x轴上,且BC=AB时(如图1),
∵OC⊥x轴,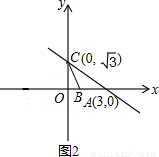
∴点O是AB的中点,
∵点A(3,0),
∴B(-3,0);
当BC=AB时(如图2),设B(a,0),则a2+( )2=(3-a)2,解得a=1,
)2=(3-a)2,解得a=1,
∴B(1,0);
当点B在y轴上时(如图3):
∵∠CAO=30°,∠AOC=90°,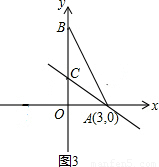
∴∠ACO=60°,
∴∠BCA=180°-∠ACO=180°-60°=120°,
若BC=AC,则∠BAC=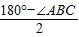 =
=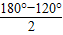 =30°,
=30°,
∴此种情况符合题意,
设点B(0,y),则(y- )2=32+(
)2=32+(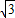 )2,解得y=3
)2,解得y=3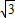 ,
,
∴B(0,3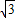 ).
).
综上所述,符合条件的B点坐标为:(-3,0);(0,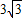 );(1,0).
);(1,0).
故答案为:(-3,0);(0,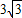 );(1,0).
);(1,0).
点评:本题考查的是一次函数综合题,涉及到一次函数的性质、等腰三角形的性质、锐角三角函数的定义及特殊角的三角函数值,根据题意画出图形,利用数形结合求解是解答此题的关键.
解答:
 解:∵直线
解:∵直线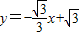 交x轴于点A,交y轴于点C,
交x轴于点A,交y轴于点C,∴A(3,0),B(0,
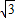 ),
),∵OC=
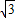 ,OA=3,
,OA=3,∴tan∠CAO=
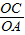 =
=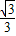 ,
,∴∠CAO=30°,
当点B在x轴上,且BC=AB时(如图1),
∵OC⊥x轴,

∴点O是AB的中点,
∵点A(3,0),
∴B(-3,0);
当BC=AB时(如图2),设B(a,0),则a2+(
 )2=(3-a)2,解得a=1,
)2=(3-a)2,解得a=1,∴B(1,0);
当点B在y轴上时(如图3):
∵∠CAO=30°,∠AOC=90°,

∴∠ACO=60°,
∴∠BCA=180°-∠ACO=180°-60°=120°,
若BC=AC,则∠BAC=
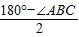 =
=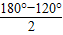 =30°,
=30°,∴此种情况符合题意,
设点B(0,y),则(y-
 )2=32+(
)2=32+(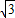 )2,解得y=3
)2,解得y=3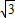 ,
,∴B(0,3
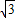 ).
).综上所述,符合条件的B点坐标为:(-3,0);(0,
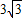 );(1,0).
);(1,0).故答案为:(-3,0);(0,
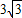 );(1,0).
);(1,0).点评:本题考查的是一次函数综合题,涉及到一次函数的性质、等腰三角形的性质、锐角三角函数的定义及特殊角的三角函数值,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 交y轴于点A,交x轴于点B,交双曲线
交y轴于点A,交x轴于点B,交双曲线 于点D,DC⊥x轴,垂足为C,且S△OAB=2S△OCD,则k=________.
于点D,DC⊥x轴,垂足为C,且S△OAB=2S△OCD,则k=________.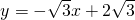 交x轴于点A,交y轴于点B,过B点的直线y=x+n交x轴于点C.
交x轴于点A,交y轴于点B,过B点的直线y=x+n交x轴于点C.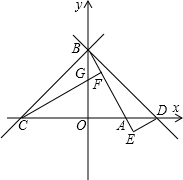
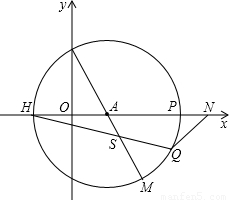
 上存在任一点Q,连接MQ并延长交x轴于点N,连接HQ交BM于S,现有两个结论 ①AN+AS的值不变; ②AN-AS的值不变,其中只有一个正确,请选择正确的结论进行证明,并求其值.
上存在任一点Q,连接MQ并延长交x轴于点N,连接HQ交BM于S,现有两个结论 ①AN+AS的值不变; ②AN-AS的值不变,其中只有一个正确,请选择正确的结论进行证明,并求其值.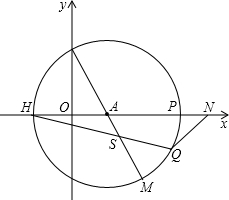
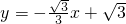 交x轴于点A,交y轴于点C,点B在坐标轴上,△ABC为等腰三角形,且底角等于30°,则点B的坐标为________.
交x轴于点A,交y轴于点C,点B在坐标轴上,△ABC为等腰三角形,且底角等于30°,则点B的坐标为________.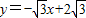 交x轴于点A,交y轴于点B,过B点的直线y=x+n交x轴于点C.
交x轴于点A,交y轴于点B,过B点的直线y=x+n交x轴于点C.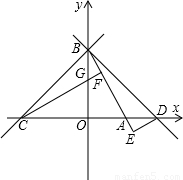
 上存在任一点Q,连接MQ并延长交x轴于点N,连接HQ交BM于S,现有两个结论 ①AN+AS的值不变; ②AN-AS的值不变,其中只有一个正确,请选择正确的结论进行证明,并求其值.
上存在任一点Q,连接MQ并延长交x轴于点N,连接HQ交BM于S,现有两个结论 ①AN+AS的值不变; ②AN-AS的值不变,其中只有一个正确,请选择正确的结论进行证明,并求其值.