题目内容
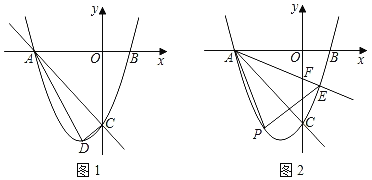
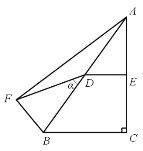
【题目】如图，Rt△ABC中，∠C=90°，BC=6，DE是△ABC的中位线，点D在AB上，把点B绕点D按顺时针方向旋转α（0°<α<180°）角得到点F，连接AF，BF．下列结论：①△ABF是直角三角形；②若△ABF和△ABC全等，则α=2∠BAC或2∠ABC；③若α=90°，连接EF，则S△DEF=4.5；其中正确的结论是（ ）
A.①②B.①③C.①②③D.②③
【答案】C
【解析】
①根据直角三角形斜边中线的性质和旋转的性质得出
，然后利用等腰三角形的性质和三角形内角和定理即可判断；
②分两种情况讨论：
或
，分别求α即可 ；
③先根据题意画出图形，首先证明
，然后得出
，最后利用
即可求解．
①∵DE是△ABC的中位线，
．
由旋转可知
，
，
．
，
，
即
，
∴△ABF是直角三角形，故①正确；
，
．
若△ABF和△ABC全等，
当时，
；
当时，
，
综上所述，若△ABF和△ABC全等，则α=2∠BAC或2∠ABC，故②正确；
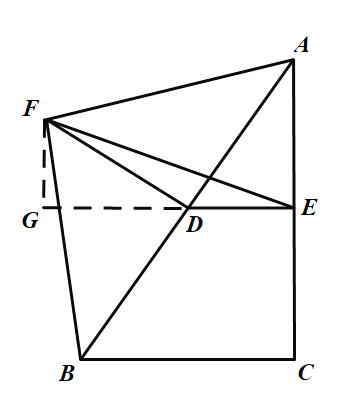
过点F作
交ED的延长线于点G，
∵DE是
的中位线，
，
．
，
．
，
，
．
，
．
，D为AB中点，
．
在
和
中，
，
，故③正确；
所以正确的有：①②③．
故选：C．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
