Question

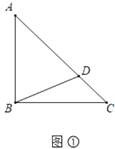
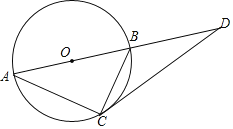
【题目】如图，已知AB是⊙O的直径，DC与⊙O相切于点C，交AB的延长线于点D．

（1）求证：∠BAC＝∠BCD；

（2）若BD＝4，DC＝6，求⊙O的半径．

Answer 1

【答案】（1）见详解；（2）⊙O的半径为．

【解析】

（1）根据直径所对的圆周角为直角以及圆的切线垂直于经过切点的半径，可得∠OCD＝∠OCB+BCD＝90°，∠ACB＝∠OCB+ACO＝90°，于是∠ACO＝∠BCD，又OA＝OC，所以∠ACO＝∠BAC，因此∠BAC＝∠BCD；

（2）易证△CDB∽△ADC，由BD＝4，DC＝6通过相似比求出DA的长，然后求出AB，从而求出⊙O的半径．

解：（1）如图，连接OC．

证明：∵DC与⊙O相切，

∠OCD＝∠OCB+∠BCD＝90°，

∵AB是⊙O的直径，

∴∠ACB＝∠OCB+∠ACO＝90°，

∴∠ACO＝∠BCD

∵OA＝OC，

∴∠ACO＝∠BAC，

∴∠BAC＝∠BCD；

（2）由（1）可得，∠BAC＝∠BCD；

∵∠CDB＝∠ADC，

∴△CDB∽△ADC，

∴ 即

∴DA＝9

∴AB＝DA﹣BD＝9﹣4＝5，

∴⊙O的半径为．