题目内容
如果我们定义:“到三角形的两个顶点距离相等的点,叫做此三角形的开心点。”那么:

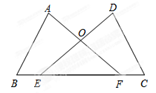
(1)如图1,观察并思考,△ABC的开心点有 个
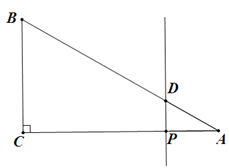
(2)如图2,CD为等边三角形ABC的高,开心点P在高CD上,且PD= ,则∠APB的度数为
,则∠APB的度数为
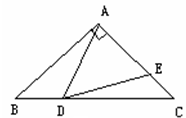
(3)已知△ABC为直角三角形,斜边BC=5,AB=3,开心点P在AC边上,试探究PA的长。

(1)如图1,观察并思考,△ABC的开心点有 个
(2)如图2,CD为等边三角形ABC的高,开心点P在高CD上,且PD=
 ,则∠APB的度数为
,则∠APB的度数为 (3)已知△ABC为直角三角形,斜边BC=5,AB=3,开心点P在AC边上,试探究PA的长。
(1)无数;(2)90°;(3)2或 .
.
 .
.试题分析:(1)根据线段垂直平分线的性质可知,△ABC的开心点有无数个;(2)连接PA、PB,根据开心点的定义,分①PB=PC,②PA=PC,③PA=PB三种情况利用等边三角形的性质求出PD与AB的关系,然后判断出只有情况③是合适的,再根据等腰直角三角形的性质求出∠APB=45°,然后即可求出∠APB的度数;(3)先根据勾股定理求出AC的长度,根据开心点的定义,分①PB=PC,②PA=PC,③PA=PB三种情况,根据三角形的性质计算即可得解.
试题解析:(1)无数.
(2)①若PB=PC,连接PB,则∠PCB=∠PBC,
∵CD为等边三角形的高,∴AD=BD,∠PCB=30°.
∴∠PBD=∠PBC=30°,∴PD=
 DB=
DB= AB.与已知PD=
AB.与已知PD= AB矛盾,∴PB≠PC.
AB矛盾,∴PB≠PC.②若PA=PC,连接PA,同理可得PA≠PC.
③若PA=PB,由PD=
 AB,得PD="AD" =BD,∴∠APD=∠BPD="45°." ∴∠APB=90°.
AB,得PD="AD" =BD,∴∠APD=∠BPD="45°." ∴∠APB=90°.(3)∵BC=5,AB=3,∴AC=
 .
.①若PB=PC,设PA=
 ,则
,则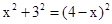 ,∴
,∴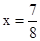 ,即PA=
,即PA= .
.②若PA=PC,则PA=2.
③若PA=PB,由图知,在Rt△PAB中,不可能.
∴PA=2或
 .
.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目