Question

如图，∠AOB=30°，点P在∠AOB内，点E、F分别在边OA、OB上移动，如果OP=3，则△PEF周长的最小值是________．

Answer 1

3
分析：作点P关于OA对称的点P₁，作点P关于OB对称的点P₂，连接P₁P₂，与OA交于点E，与OB交于点F，此时△PEF的周长最小，然后根据∠AOB=30°，点P在∠AOB内，点E、F分别在边OA、OB上移动，如果OP=3，可求出值．
解答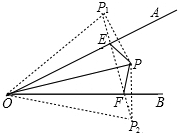：解：作点P关于OA对称的点P₁，作点P关于OB对称的点P₂，连接P₁P₂，与OA交于点E，与OB交于点F，此时△PEF的周长最小．
从图上可看出△PEF的周长就是P₁P₂的长，
∵∠AOB=30°，
∴∠P₁OP₂=60°．
∵OP₁=OP₂，
∴△OP₁P₂是等边三角形．
∴P₁P₂=OP₁=OP=3．
∴△PEF周长的最小值是3．
故答案为：3．
点评：本题考查轴对称最短路径问题，关键是确定E，F的值，然后找到最小周长的三角形，然后求出最小周长．