Question

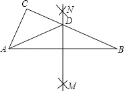
【题目】将一块正方形和一块等腰直角三角形如图1摆放．

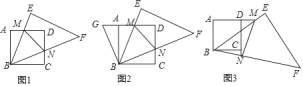
（1）如果把图1中的△BCN绕点B逆时针旋转90°，得到图2，则∠GBM=　 　；

（2）将△BEF绕点B旋转．

①当M，N分别在AD，CD上（不与A，D，C重合）时，线段AM，MN，NC之间有一个不变的相等关系式，请你写出这个关系式：　 　；（不用证明）

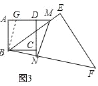
②当点M在AD的延长线上，点N在DC的延长线时（如图3），①中的关系式是否仍然成立？若成立，写出你的结论，并说明理由；若不成立，写出你认为成立的结论，并说明理由．

Answer 1

【答案】(1) 45°；(2) ①见解析; ②见解析.

【解析】

（1）由旋转的性质得∠GBA=∠CBN，于是得到∠ABM+∠GBA=45°，即可得到结论；

（2）①根据旋转的性质得到∠GAB=∠C=90°，AG=CN，BG=BN，∠ABG=∠CBN，得到D，A，G三点共线，根据全等三角形的性质得到GM=MN，于是得到结论；

②在AM上截取AG，使得AG=CN，连结BG；根据正方形的性质得到AB=BC，∠A=∠BCN=90°，根据全等三角形的性质得到BG=BN，∠ABG=∠NBC，根据全等三角形的性质即可得到结论．

（1）在正方形ABCD和等腰直角△BEF中，

∵∠ABC=90°，

∴∠EBF=45°，

∴∠ABM+∠CBN=45°，

由旋转的性质得∠GBA=∠CBN，

∴∠ABM+∠GBA=45°，

即∠GBM=45°，

故答案为：45°；

（2）①AM+NC=MN；

理由：∵把图1中的△BCN绕点B逆时针旋转90°得到△ABG，

∴∠GAB=∠C=90°，AG=CN，BG=BN，∠ABG=∠CBN，

∴∠GAB+∠DAB=180°，

∴D，A，G三点共线，

∴∠ABM+∠GBA=45°，

∴∠GBM=∠MBN，

在△GBM与△NBM中，

，

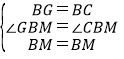∴△GBM≌△NBM，

∴GM=MN，

∵GM=AG+AM=CN+AM，

∴MN=AM+CN；

故答案为：MN=AM+CN；

②上面的式子不成立，结论是：AM﹣NC=MN，

理由：在AM上截取AG，使得AG=CN，连结BG；

∵四边形ABCD是正方形，

∴AB=BC，∠A=∠BCN=90°，

在△BAG与△BCN中，

，

∴△BAG≌△BCN，

∴BG=BN，∠ABG=∠NBC，

∴∠MBN=∠MBC+∠CBN=∠MBC+∠ABG=45°=∠GBM，

在△BGM与△BMN中，

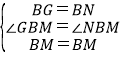
∴△BGM≌△BNM，

∴GM=NM，

∴AM﹣CN=MN．