题目内容
 如图,等腰△ABC内接于⊙O,BA=CA,弦CD平分∠ACB,交AB于点H,过点B作AD的平行线分别交AC,DC于点E,F.
如图,等腰△ABC内接于⊙O,BA=CA,弦CD平分∠ACB,交AB于点H,过点B作AD的平行线分别交AC,DC于点E,F.(1)求证:CF=BF;
(2)若BH=DH=1,求FH的值.
分析:(1)根据CD平分∠ACB,利用圆周角定理,求证BE∥AD,再根据等腰三角形的性质和等量代换即可求证CF=BF.
(2)连接DB,根据BH=DH,求证∠FHB=2∠HBD,同理,∠HFB=2∠FCB,再求证△FBH∽△FDB,然后利用相似三角形对应边成比例即可求得FH的值.
(2)连接DB,根据BH=DH,求证∠FHB=2∠HBD,同理,∠HFB=2∠FCB,再求证△FBH∽△FDB,然后利用相似三角形对应边成比例即可求得FH的值.
解答:证明:(1)∵CD平分∠ACB,
∴∠ACD=∠BCD,
∵∠BCD=∠DAB,
∴∠ACD=∠DAB,
∴BE∥AD,
∴∠EBA=∠DAB,
∴∠ACD=∠ABE,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠FCB=∠FBC,
∴CF=BF;
(2)连接DB,∵BH=DH,
∴∠HDB=∠HBD,
∴∠FHB=2∠HBD,
同理,∠HFB=2∠FCB,
∵∠ABD=∠ACD=∠DCB,
∴∠FHB=∠HFB,
∴FB=HB=1,
∵FB∥AD,
∴∠1=∠2,
∵DC平分∠ACB,
∴
=
,
∴∠1=∠3,
∴∠2=∠3,
∴△FBH∽△FDB,
∴
=
,
设FH=x,则FD=x+1,
∴
=
,
解之得,x=
,
即FH=
∴∠ACD=∠BCD,
∵∠BCD=∠DAB,
∴∠ACD=∠DAB,
∴BE∥AD,
∴∠EBA=∠DAB,
∴∠ACD=∠ABE,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠FCB=∠FBC,
∴CF=BF;
(2)连接DB,∵BH=DH,
∴∠HDB=∠HBD,
∴∠FHB=2∠HBD,
同理,∠HFB=2∠FCB,
∵∠ABD=∠ACD=∠DCB,

∴∠FHB=∠HFB,
∴FB=HB=1,
∵FB∥AD,
∴∠1=∠2,
∵DC平分∠ACB,
∴
 |
| AD |
 |
| DB |
∴∠1=∠3,
∴∠2=∠3,
∴△FBH∽△FDB,
∴
| FH |
| FB |
| FB |
| FD |
设FH=x,则FD=x+1,
∴
| x |
| 1 |
| 1 |
| x+1 |
解之得,x=
| ||
| 2 |
即FH=
| ||
| 2 |
点评:此题主要考查学生对相似三角形的判定与性质,等腰三角形的性质,平行线的性质,圆周角定理的理解和掌握,涉及到知识点较多,综合性较强,有一定的难度.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
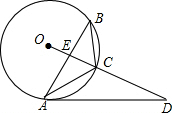 已知:如图,等腰△ABC内接于⊙O,点D在OC的延长线上,连接AD,交AB于点E,∠D=40°,∠B=25°.
已知:如图,等腰△ABC内接于⊙O,点D在OC的延长线上,连接AD,交AB于点E,∠D=40°,∠B=25°.(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为5,求弦AB的长(结果精确到0.01).
 已知如图,等腰△ABC内接于⊙O,∠B=∠ACB=30°,弦AD交BC于E,AE=2,ED=4,则⊙O的半径为
已知如图,等腰△ABC内接于⊙O,∠B=∠ACB=30°,弦AD交BC于E,AE=2,ED=4,则⊙O的半径为 已知:如图,等腰△ABC内接于⊙O,点D在OC的延长线上,连接AD,交AB于点E,∠D=40°,∠B=25°.
已知:如图,等腰△ABC内接于⊙O,点D在OC的延长线上,连接AD,交AB于点E,∠D=40°,∠B=25°.