题目内容
已知在平面直角坐标系中,直线 与x轴,y轴相交于A,B两点,直线
与x轴,y轴相交于A,B两点,直线 与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运动到点A,过点D作x轴的垂线,分别交直线
与AB相交于C点,点D从点O出发,以每秒1个单位的速度沿x轴向右运动到点A,过点D作x轴的垂线,分别交直线 和直线
和直线 于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒)
于P,Q两点(P点不与C点重合),以PQ为边向左作正△PQR,设正△PQR与△OBC重叠部分的面积为S(平方单位),点D的运动时间为t(秒)(1)求点A,B,C的坐标;
(2)若点M(2,3
 )正好在△PQR的某边上,求t的值;
)正好在△PQR的某边上,求t的值;(3)求S关于t的函数关系式,并写出相应t的取值范围,求出D在整个运动过程中s的最大值.

【答案】分析:(1)令y=0,可求A点的横坐标;令x=0,可求B点的横坐标;直线 与直线
与直线 联立可求C点坐标;
联立可求C点坐标;
(2)本题只需考虑点M(2,3 )正好在△PQR的某边上,求出t的取值即可.
)正好在△PQR的某边上,求出t的取值即可.
(3)本题要分5种情况进行讨论.当0≤t≤ 时;当
时;当 <t<3时;当t=3时;当3<t≤
<t<3时;当t=3时;当3<t≤ 时;当
时;当 ≤t≤6时.讨论求出S的最大取值.
≤t≤6时.讨论求出S的最大取值.
解答:解:(1)令y=0,可求A点的横坐标为:6;
故A点坐标为;(6,0),
令x=0,可求B点的纵坐标为:(0,6 );
);
直线 与直线
与直线 联立可求C点坐标为:(3,3
联立可求C点坐标为:(3,3 );
);
(2)当M在QP上或在RQ上以及RP上时,
分别求出: ,
, ,t3=2;
,t3=2;
(3)
 ,
,
因为S的最大值在 范围内取到,
范围内取到, ,开口向下,对称轴直线x=9,函数的自变量
,开口向下,对称轴直线x=9,函数的自变量 部分图象在对称轴的左侧,S随t的增大而增大
部分图象在对称轴的左侧,S随t的增大而增大
故当t=6时, .
.
点评:考查了一次函数综合题.本题中对于点的运动要分类进行讨论.分类讨论是初中数学重要的思想方法,难点是一要想到用讨论的方法进行求解.而是讨论界限要确定不要漏解和重复.
 与直线
与直线 联立可求C点坐标;
联立可求C点坐标;(2)本题只需考虑点M(2,3
 )正好在△PQR的某边上,求出t的取值即可.
)正好在△PQR的某边上,求出t的取值即可.(3)本题要分5种情况进行讨论.当0≤t≤
 时;当
时;当 <t<3时;当t=3时;当3<t≤
<t<3时;当t=3时;当3<t≤ 时;当
时;当 ≤t≤6时.讨论求出S的最大取值.
≤t≤6时.讨论求出S的最大取值.解答:解:(1)令y=0,可求A点的横坐标为:6;
故A点坐标为;(6,0),
令x=0,可求B点的纵坐标为:(0,6
 );
);直线
 与直线
与直线 联立可求C点坐标为:(3,3
联立可求C点坐标为:(3,3 );
);(2)当M在QP上或在RQ上以及RP上时,
分别求出:
 ,
, ,t3=2;
,t3=2;(3)
 ,
,因为S的最大值在
 范围内取到,
范围内取到, ,开口向下,对称轴直线x=9,函数的自变量
,开口向下,对称轴直线x=9,函数的自变量 部分图象在对称轴的左侧,S随t的增大而增大
部分图象在对称轴的左侧,S随t的增大而增大故当t=6时,
 .
.点评:考查了一次函数综合题.本题中对于点的运动要分类进行讨论.分类讨论是初中数学重要的思想方法,难点是一要想到用讨论的方法进行求解.而是讨论界限要确定不要漏解和重复.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
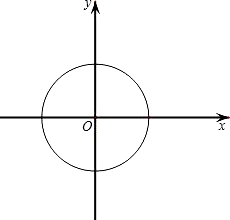 已知在平面直角坐标系xOy中,⊙O的半径为1.
已知在平面直角坐标系xOy中,⊙O的半径为1.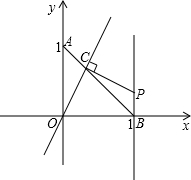 直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y),
直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y), 如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.
如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.