Question

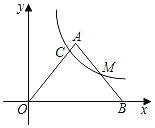
【题目】如图，在平面直角坐标系中，△OAB的边OB在x轴的正半轴上，AO＝AB，M是边AB的中点，经过点M的反比例函数y＝（k＞0，x＞0）的图象与边OA交于点C，则的值为__．

Answer 1

【答案】

【解析】

过点C、点A、点M作x轴的垂线CD、AE、MF，由平行线截线段成比例定理可得＝＝；再由三角形的中位线定理得出MF＝AE，EF＝BF＝BE＝OE，从而OF＝OE；由点C和点M均在反比例函数y＝（k＞0，x＞0）的图象上，得出ODCD＝OFMF＝k，将前面所得的相关线段的数量关系代入化简，得出·＝，则可求得答案．

解：如图，过点C、点A、点M作x轴的垂线CD、AE、MF，

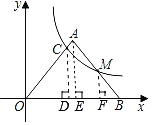
则CD∥AE∥MF，

∴＝＝，

∵AO＝AB，AE⊥x轴，

∴OE＝BE，

∵M是边AB的中点，MF∥AE，

∴MF＝AE，EF＝BF＝BE＝OE，

∴OF＝OE，

∵点C和点M均在反比例函数y＝（k＞0，x＞0）的图象上，

∴ODCD＝OFMF＝k，

∴ODCD＝OE×AE，

∴＝，

∵＝＝，

∴·＝，

∴＝，（负值舍去）．

故答案为：．