题目内容
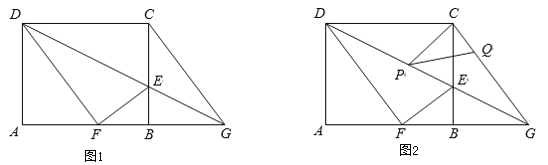
【题目】如图1,平面内有一点![]() 到
到![]() 的三个顶点的距离分别为
的三个顶点的距离分别为![]() 若有
若有![]() ,则称点
,则称点![]() 为
为![]() 关于点
关于点![]() 的勾股点.
的勾股点.
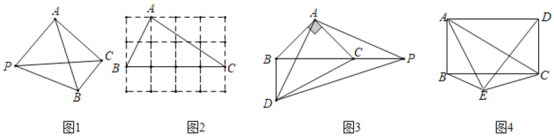
![]() 如图2,在
如图2,在![]() 的方格纸中,每个小正方形的边长均为
的方格纸中,每个小正方形的边长均为![]() 的顶点在格点上,请找出所有的格点
的顶点在格点上,请找出所有的格点![]() ,使点
,使点![]() 为
为![]() 关于点
关于点![]() 的勾股点;
的勾股点;
![]() 如图3,
如图3, ![]() 为等腰直角三角形,
为等腰直角三角形,![]() 是斜边
是斜边![]() 延长线上一点,连接
延长线上一点,连接![]() ,以
,以![]() 为直角边作等腰直角三角形
为直角边作等腰直角三角形 ![]() (点
(点![]() 顺时针排列),
顺时针排列),![]() ,连接
,连接 ![]() 求证:点
求证:点![]() 为
为![]() 关于点
关于点![]() 的勾股点;
的勾股点;
![]() 如图4,点
如图4,点![]() 是矩形
是矩形![]() 外一点,且点
外一点,且点![]() 是
是![]() 关于点
关于点![]() 的勾股点,若
的勾股点,若![]() ,求
,求![]() 的长.
的长.
【答案】![]() 见解析;
见解析;![]() 见解析;
见解析;![]()
![]()
【解析】
(1)如图1,图2,求出PA2,PB2,PC2,得到PC2+PB2=PA2,即得出点P是△ABC关于点A的勾股点;
(2)证明△ABD≌△ACP(SAS),得出BD=CP,∠ABD=∠ACP=135°,证明∠DBP=90°,则结论得证;
(3)由条件“点C是△ABE关于点A的勾股点”可得CE=CD=5,如图3,过点E作MN⊥AB于点M,交DC的延长线于点N,设AM=DN=x,则CN=DN-CD=x-5,由勾股定理可得62-x2=52-(x-5)2,解得:x=![]() ,则求出AM,ME的长,则答案可得出.
,则求出AM,ME的长,则答案可得出.
(1)如图1,
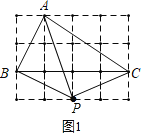
∵PA2=12+32=10,PB2=12+22=5,PC2=PB2=5,
∴PA2=PC2+PB2,
∴点P是△ABC关于点A的勾股点;
如图2,
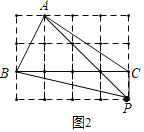
∵PA2=32+32=18,PB2=12+42=17,PC2=1,
∴PA2=PC2+PB2,
∴点P是△ABC关于点A的勾股点;
(2)∵△ABC和△APD为等腰直角三角形,
∴AB=AC,AD=AP,∠BAC=∠DAP=90°,
∴∠BAC-∠DAC=∠DAP-∠DAC,
即∠BAD=∠CAP,
∴△ABD≌△ACP(SAS),
∴BD=PC,∠ABD=∠ACP=135°,
∵∠ABC=45°,
∴∠DBP=∠ABD-∠ABC=135°-45°=90°,
∴BD2+PB2=PD2,
∴PC2+PB2=PD2,
∴点P为△BDC关于点D的勾股点.
(3)解:∵矩形ABCD中,AD=8,
∴AD=BC=8,CD=AB,
∵AD=DE,
∴DE=8,
∵点C是△ABE关于点A的勾股点,
∴AC2=CB2+CE2,
∵AC2=AB2+BC2,
∴CE=CD=5,
如图3,过点E作MN⊥AB于点M,交DC的延长线于点N,
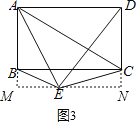
∴∠AME=∠MND=90°,
∴四边形AMND是矩形,
∴MN=AD=8,AM=DN,
设AM=DN=x,则CN=DN-CD=x-5,
∵Rt△DEN中,EN2+DN2=DE2;Rt△CEN中,EN2+CN2=CE2,
∴DE2-DN2=CE2-CN2,
∴62-x2=52-(x-5)2
解得:x=![]() ,
,
∴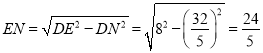 ,
,![]() ,
,
∴![]() ,
,
∴Rt△AME中,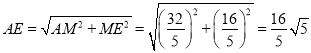 .
.

【题目】国务院发布的《全民科学素质行动计划纲要实施方案(2016-2020年)》指出:公民科学素质是实施创新驱动发展战略的基础,是国家综合国力的体现.《方案》明确提出,2020年要将我国公民科学素质的数值提升到10%以上.为了解我国公民科学素质水平及发展状况,中国科协等单位已多次组织了全国范围的调查,以下是根据调查结果整理得到的部分信息.注:科学素质的数值是指具备一定科学素质的公民人数占公民总数的百分比.
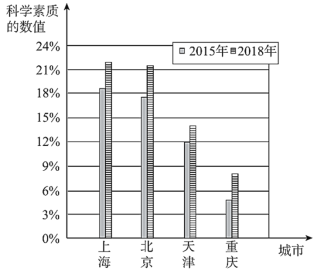
![]() .2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
.2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
b.2015年和2018年我国公民科学素质发展状况按性别分类统计如下:
2015年 | 2018年 | |
男 |
|
|
女 |
|
|
c.2001年以来我国公民科学素质水平发展统计图如下:
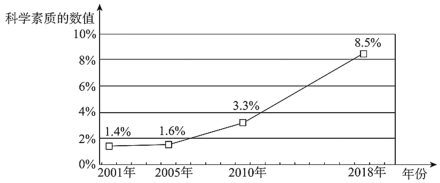
根据以上信息,回答下列问题:
(1)在我国四个直辖市中,从2015年到2018年,公民科学素质水平增幅最大的城市是________,公民科学素质水平增速最快的城市是_________.注:科学素质水平增幅=2018年科学素质的数值一2015年科学素质的数值;科学素质水平增速=(2018年科学素质的数值一2015年科学素质的数值)÷2015年科学素质的数值.
(2)已知在2015年的调查样本中,男女公民的比例约为1:1,则2015年我国公民的科学素质水平为______%(结果保留一位小数);由计算可知.在2018年的调查样本中.男性公民人数_____女性公民人数(填“多于”、“等于”或“少于”).
(3)根据截至2018年的调查数据推断,你认为“2020年我国公民科学素质提升到10%以上”的目标能够实现吗?请说明理由.
【题目】如图1,P是△ABC外部的一定点,D是线段BC上一动点,连接PD交AC于点E.
小明根据学习函数的经验,对线段PD,PE,CD的长度之间的关系进行了探究,
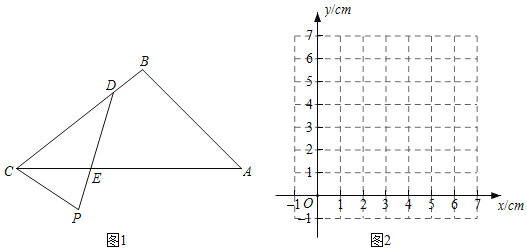
下面是小明的探究过程,请补充完整:
(1)对于点D在BC上的不同位置,画图、测量,得到了线段PD,PE,CD的长度的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
PD/cm | 2.56 | 2.43 | 2.38 | 2.43 | 2.67 | 3.16 | 3.54 | 4.45 | 5.61 |
PE/cm | 2.56 | 2.01 | 1.67 | 1.47 | 1.34 | 1.32 | 1.34 | 1.40 | 1.48 |
CD/cm | 0.00 | 0.45 | 0.93 | 1.40 | 2.11 | 3.00 | 3.54 | 4.68 | 6.00 |
在PD,PE,CD的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出图2中所确定的两个函数的图象;
(3)结合函数图象,解决问题:
连接CP,当△PCD为等腰三角形时,CD的长度约为 cm.(精确到0.1)