题目内容
6.已知x2-x=5,求代数式(x+2)2-x(3+2x)的值.分析 原式第一项利用完全平方公式化简,第二项利用单项式乘以多项式法则计算,去括号合并得到最简结果,把已知等式代入计算即可求出值.
解答 解:原式=x2+4x+4-3x-2x2=-x2+x+4,
∵x2-x=5,
∴原式=-(x2-x)+4=-5+4=-1.
点评 此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
17.4的相反数是( )
| A. | -4 | B. | 4 | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |
14.若分式$\frac{x-2}{x-1}$的值为0,则x的值为( )
| A. | 1或2 | B. | 2 | C. | 1 | D. | 0 |
18.若$\sqrt{m-8}$+|n-2|=0,且关于x的一元二次方程ax2+mx+n=0有实数根,则a的取值范围是( )
| A. | a≥8 | B. | a<8且a≠0 | C. | a≤8 | D. | a≤8且a≠0 |
10.在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(1)请估计:当实验次数为5000次时,摸到白球的频率将会接近0.6;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)=0.6;
(3)试验估算这个不透明的盒子里黑球有多少只?
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(2)假如你摸一次,你摸到白球的概率P(摸到白球)=0.6;
(3)试验估算这个不透明的盒子里黑球有多少只?
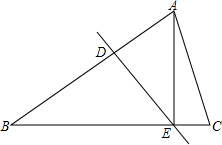 如图所示,△ABC中,DE垂直平分AB,分别交AB、BC于点D、E
如图所示,△ABC中,DE垂直平分AB,分别交AB、BC于点D、E