题目内容
7. 如图,直角坐标系中,在边长为1的正方形网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,1),B(2,3).
如图,直角坐标系中,在边长为1的正方形网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,1),B(2,3).(1)请在图中画出△AOB关于y轴的对称△A′OB′,点A′的坐标为(-3,1),点B′的坐标为(-2,3);
(2)请写出A′点关于x轴的对称点A′'的坐标为(-3,-1);
(3)求△A′OB′的面积.
分析 (1)根据网格结构找出点A′、B′的位置,然后与点O顺次连接即可,再根据平面直角坐标系写出点A′、B′的坐标;
(2)根据关于x轴对称的点的横坐标相同,纵坐标互为相反数写出即可;
(3)利用三角形所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解.
解答 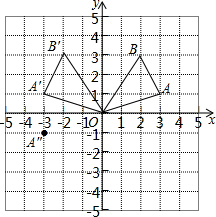 解:(1)△A'O B'如图所示;点A'(-3,1),B'(-2,3);
解:(1)△A'O B'如图所示;点A'(-3,1),B'(-2,3);
(2)A''(-3,-1);
(3)S△A'OB′=3×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×1×3-$\frac{1}{2}$×3×2,
=9-1-$\frac{3}{2}$-3,
=$\frac{7}{2}$.
故答案为:(1)(-3,1),(-2,3);(2)(-3,-1).
点评 本题考查了利用轴对称变换作图,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
2.下列各曲线中,不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
12.下列四个图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.下列各式计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$ | C. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{3}$ |