题目内容
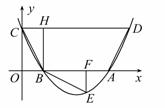
如图,抛物线 与
与 轴交于A、B两点,与y轴交于C点,且
轴交于A、B两点,与y轴交于C点,且 .
.
【小题1】求抛物线的解析式及顶点D的坐标;
【小题2】点
 是
是 轴上的一个动点,当的
轴上的一个动点,当的 值最小
值最小时,求
 的值.
的值.
【小题1】∵点
 在抛物线
在抛物线 上,
上,∴
 ,解得b =
,解得b =
∴抛物线的解析式为y=
 x2-
x2- x-2. y=
x-2. y= x2-
x2- x-2 =
x-2 = ( x2 -3x- 4 ) =
( x2 -3x- 4 ) = ,
,∴顶点D的坐标为 (
 ,-
,- ).
).【小题2】设点C关于x轴的对称点为
 ,直线
,直线 的解析式为y =" kx" + n,
的解析式为y =" kx" + n,
则
 ,解得n = 2,
,解得n = 2, .
.∴
 .
.∴当y = 0时,
 ,
, .∴
.∴ .解析:
.解析:(1)把A点坐标代入解出抛物线的解析式,通过抛物线的函数性质求出顶点D的坐标;
(2)作C点关于x轴的对称点C′,C′D是
 最小值,然后求出C′D与x轴的交点M的坐标。
最小值,然后求出C′D与x轴的交点M的坐标。 
练习册系列答案
相关题目
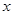 轴交于
轴交于 (2)点
(2)点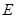 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以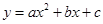 与
与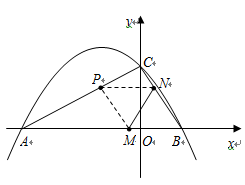
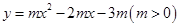 与
与 轴交于
轴交于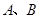 两点,与
两点,与 轴交于
轴交于 点.
点.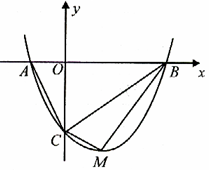
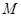 的坐标(用含
的坐标(用含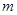 的代数式表示),
的代数式表示), 与
与 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;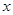 轴交于
轴交于 (
( ,0)、
,0)、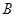 (
( ,0)两点,且
,0)两点,且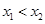 ,与
,与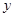 轴交于点
轴交于点 ,其中
,其中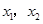 是方程
是方程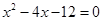 的两个根。(14分)
的两个根。(14分) (2)点
(2)点 是线段
是线段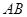 上的一个动点,过点
上的一个动点,过点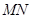 ∥
∥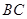 ,交
,交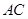 于点
于点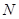 ,连接
,连接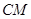 ,当
,当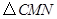 的面积最大时,求点
的面积最大时,求点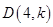 在(1)中抛物线上,
在(1)中抛物线上,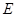 为抛物线上一动点,在
为抛物线上一动点,在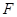 ,使以
,使以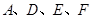 为顶
为顶