Question

【题目】某校为进一步推进“一校一球队、一级一专项、一人一技能”的体育活动，决定对学生感兴趣的球类项目（A：足球，B：篮球，C：排球，D：羽毛球，E：乒乓球）进行问卷调查，学生可根据自己的喜好选修一门，李老师对某班全班同学的选课情况进行统计后，制成了两幅不完整的统计图（如图）．

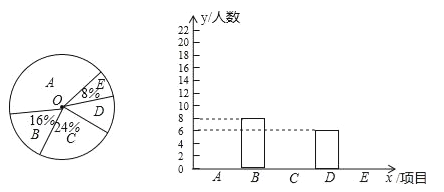
（1）该班对足球和排球感兴趣的人数分别是　 　、　 　；

（2）若该校共有学生3500名，请估计有多少人选修足球？

（3）该班班委5人中，1人选修篮球，3人选修足球，1人选修排球，李老师要从这5人中任选2人了解他们对体育选修课的看法，请你用列表或画树状图的方法，求选出的2人恰好1人选修篮球，1人选修足球的概率．

Answer 1

【答案】（1）20、12；（2）1400；（3）

【解析】试题分析：（1）先利用B的人数和所占的百分比计算出全班人数，再利用C、E的百分比计算出C、E的人数，则用全班人数分别减去B、C、D、E的人数得到A的人数；

（2）根据样本估计总体，用3500乘以样本中足球人数所占比例即可得到选修足球的人数；

（3）先利用树状图展示所有20种等可能的结果数，找出选出的2人恰好1人选修篮球，1人选修足球所占结果数，然后根据概率公式求解．

试题解析：解：（1）∵该班人数为8÷16%=50（人），∴C的人数=24%×50=12（人），E的人数=8%×50=4（人），∴A的人数=50﹣8﹣12﹣4﹣6=20（人）．故答案为：20、12；

（2）3500×=1400（人）．

答：估计有1400人选修足球；

（3）画树状图：

共有20种等可能的结果数，其中选出的2人恰好1人选修篮球，1人选修足球占6种，所以选出的2人恰好1人选修篮球，1人选修足球的概率==．