Question

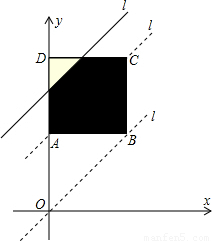
（2004•郑州）如图，边长为2的正方形ABCD中，顶点A的坐标是（0，2），一次函数y=x+t的图象l随t的不同取值变化时，位于l的右下方由l和正方形的边围成的图形面积为S（阴影部分）．
（1）当t何值时，S=3；
（2）在平面直角坐标系下，画出S与t的函数图象．

Answer 1

【答案】分析：（1）先证Rt△DMN是等腰三角形，再求得当△DMN的面积是1时，MD的值，最后得出s=3时，t的取值；
（2）分两种情况讨论s的解析式，有解析式可画出函数图象．
解答：解：如图．
（1）设l与正方形的边AD、CD相交于M、N，易证Rt△DMN是等腰三角形，
只有当MD=时，△DMN的面积是1，
求得t=4-．
容易验证，此时的S=3．
∴当t=4-时，S=3；

（2）当0≤t＜2时，S=t²
当2≤t＜4时，S=-（t-4）²+4
当t＞4时，S=4．
根据以上解析式，作图如图．

点评：本题涉及一次函数的综合知识，难度中上．