Question

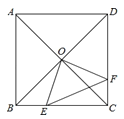
【题目】如图，两车分别从路段AB两端同时出发，沿平行路线AC、BD行驶，CE和DF的长分别表示两车到道路AB的距离．

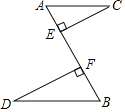
（1）求证：△ACE∽△BDF；

（2）如果两车行驶速度相同，求证：△ACE≌△BDF．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）利用平行线的性质得出∠A＝∠B，根据CE和DF的长分别表示两车到道路AB的距离可得∠CEA＝∠DFB＝90°，利用相似三角形的判定方法即可得出答案；
（2）由题意可得AC＝BD，利用全等三角形的判定方法AAS即可得出答案．

（1）证明：∵AC∥BD，

∴∠A＝∠B，

∵CE⊥AB，DF⊥AB，

∴∠CEA＝∠DFB＝90°

∴△ACE∽△BDF；

（2）证明：由(1)得: ∠A＝∠B，∠CEA＝∠DFB

∵两车等速同时行驶

∴AC＝BD

在△ACE和△BDF中

∴△ACE≌△BDF（AAS）