Question

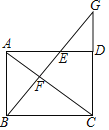
【题目】如图，在矩形ABCD中，AC为对角线，过点B作BF⊥AC于点F，延长BF交AD于点E，交CD的延长线于点G．

（1）求证：△ABF∽△EGD；

（2）若CD＝5，DG＝3，求tan∠GBC的值．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）在矩形ABCD中，∠BAD＝∠BCD＝∠ADC＝90°，AB＝CD，AB∥GC，由于∠AFB＝∠ADG＝90°，AB∥GC，所以∠ABF＝∠G，从而得证；

（2）由于∠BCD＝∠AFB＝90°，所以∠ACB+∠ACD＝90°，∠G+∠ACD＝90°，所以∠ACB＝∠G，又因为∠ABC＝∠BCG＝90°，从而可知△ABC∽△BCG，所以BC2＝CGAB，求出BC＝2，所以tan∠GBC＝

解：（1）在矩形ABCD中，

∠BAD＝∠BCD＝∠ADC＝90°，

AB＝CD，AB∥GC，

∵BF⊥AC

∴∠AFB＝∠ADG＝90°，

∵AB∥GC，

∴∠ABF＝∠G，

∴△ABF∽△EGD

（2）∵∠BCD＝∠AFB＝90°，

∴∠ACB+∠ACD＝90°，∠G+∠ACD＝90°，

∴∠ACB＝∠G

∵∠ABC＝∠BCG＝90°，

∴△ABC∽△BCG，

∴＝，

∴BC2＝CGAB，

∵CG＝CD+DG＝8，AB＝CD＝5，

∴BC＝2

∴tan∠GBC＝