题目内容
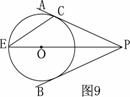
如图9所示,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切
(2)PO的延长线与⊙O交于点E,若⊙O的半径为3,PC=4.
求弦CE的长.
(1)证明:过点O作OD⊥PB,连接OC.
∵AP与⊙O相切, ∴OC⊥AP.
 又∵OP平分∠APB, ∴OD=OC.
又∵OP平分∠APB, ∴OD=OC.
∴PB是⊙O的切线.
(2)解:过C作CF⊥PE于点F.
在Rt△OCP中,OP=
∵
∴ 在Rt△COF中,
在Rt△COF中,
∴
在Rt△CFE中,

练习册系列答案
相关题目
 介于( )
介于( ) ,其中
,其中 .
. = .
= . ,则
,则 = .
= . D、-
D、- 若两个扇形满足弧长的比等于
若两个扇形满足弧长的比等于 它们半径的比,则这称这两个扇形相似。如图,如果扇形AOB与扇形
它们半径的比,则这称这两个扇形相似。如图,如果扇形AOB与扇形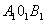 是相似扇形,且半径
是相似扇形,且半径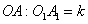 (
(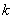 为不等于0的常数)。那么下面四个结论:
为不等于0的常数)。那么下面四个结论: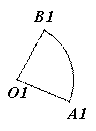
 ;
; 。成立的个数为:
。成立的个数为: 抛物线的一部分,且表达式为:
抛物线的一部分,且表达式为: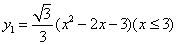 曲线
曲线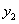 与曲线
与曲线 对称。
对称。 轴交曲线
轴交曲线 曲线
曲线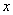 轴交于点N,试问在线段MN下方的曲线
轴交于点N,试问在线段MN下方的曲线