题目内容
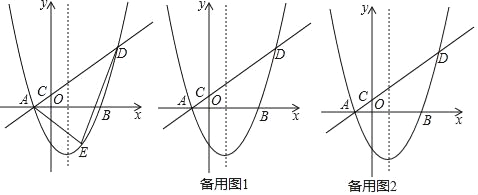
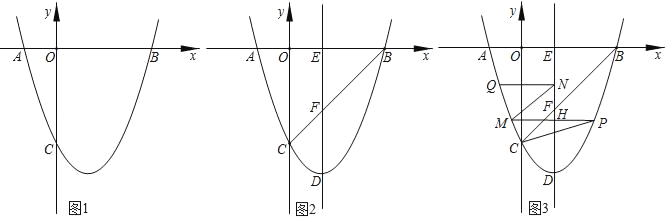
【题目】如图所示,平面直角坐标系中,O为坐标原点,二次函数![]() 的图象与x轴交于
的图象与x轴交于![]() 、B两点,与y轴交于点C;
、B两点,与y轴交于点C;
(1)求c与b的函数关系式;
(2)点D为抛物线顶点,作抛物线对称轴DE交x轴于点E,连接BC交DE于F,若AE=DF,求此二次函数解析式;
(3)在(2)的条件下,点P为第四象限抛物线上一点,过P作DE的垂线交抛物线于点M,交DE于H,点Q为第三象限抛物线上一点,作![]() 于N,连接MN,且
于N,连接MN,且![]() ,当
,当![]() 时,连接PC,求
时,连接PC,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)把A(-1,0)代入y=x2-bx+c,即可得到结论;
(2)由(1)得,y=x2-bx-1-b,求得EO=![]() ,AE=
,AE=![]() +1=BE,于是得到OB=EO+BE=
+1=BE,于是得到OB=EO+BE=![]() +
+![]() +1=b+1,当x=0时,得到y=-b-1,根据等腰直角三角形的性质得到D(
+1=b+1,当x=0时,得到y=-b-1,根据等腰直角三角形的性质得到D(![]() ,-b-2),将D(
,-b-2),将D(![]() ,-b-2)代入y=x2-bx-1-b解方程即可得到结论;
,-b-2)代入y=x2-bx-1-b解方程即可得到结论;
(3)连接QM,DM,根据平行线的判定得到QN∥MH,根据平行线的性质得到∠NMH=∠QNM,根据已知条件得到∠QMN=∠MQN,设QN=MN=t,求得Q(1-t,t2-4),得到DN=t2-4-(-4)=t2,同理,设MH=s,求得NH=t2-s2,根据勾股定理得到NH=1,根据三角函数的定义得到∠NMH=∠MDH推出∠NMD=90°;根据三角函数的定义列方程得到t1=![]() ,t2=-
,t2=-![]() (舍去),求得MN=
(舍去),求得MN=![]() ,根据三角函数的定义即可得到结论.
,根据三角函数的定义即可得到结论.
(1)把A(﹣1,0)代入![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)由(1)得,![]() ,
,
∵点D为抛物线顶点,
∴![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
将![]() 代入
代入![]() 得,
得,![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
∴二次函数解析式为:![]() ;
;
(3)连接QM,DM,
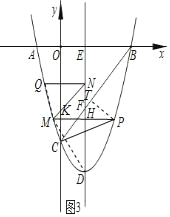
∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,设
,设![]() ,则
,则![]() ,
,
∴![]() ,同理,
,同理,
设![]() ,则
,则![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴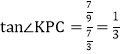 ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
过P作![]() 于T,
于T,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案