题目内容
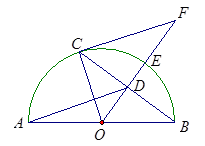
如图,AB是半圆O上的直径,E是 | BC |
 长线于点F.已知BC=8,DE=2.
长线于点F.已知BC=8,DE=2.(1)求⊙O的半径;
(2)求CF的长;
(3)求tan∠BAD的值.
分析:(1)根据垂径定理可得△BOD为直角三角形,根据勾股定理求出半径;
(2)由1得OD=3,证明△COF∽△DOC,利用线段比求出CF;
(3)过点D作DM⊥AB于M,则可求DM、OM、AM的长,则tan∠BAD的值可求.
(2)由1得OD=3,证明△COF∽△DOC,利用线段比求出CF;
(3)过点D作DM⊥AB于M,则可求DM、OM、AM的长,则tan∠BAD的值可求.
解答: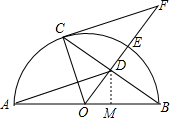 解:(1)∵E是
解:(1)∵E是
的中点,
∴OE垂直平分BC,
∴△BOD为直角三角形.
设半径为x,则BO=x,OD=x-2,BD=4,
在直角△BOD中,根据勾股定理得(x-2)2+42=x2,
解得x=5.
即⊙O的半径为5;
(2)∵∠FCO=∠CDO=90°,∠COF=∠DOC,
∴△COF∽△DOC,
∴
=
,
∴CF=
;
(3)过点D作DM⊥AB于M,
∴DM=
=
.
又∵△ODM∽△OBD,
∴OM=
.
∴tan∠BAD=
=
=
.
 解:(1)∵E是
解:(1)∵E是 |
| BC |
∴OE垂直平分BC,
∴△BOD为直角三角形.
设半径为x,则BO=x,OD=x-2,BD=4,
在直角△BOD中,根据勾股定理得(x-2)2+42=x2,
解得x=5.
即⊙O的半径为5;
(2)∵∠FCO=∠CDO=90°,∠COF=∠DOC,
∴△COF∽△DOC,
∴
| CF |
| CD |
| OC |
| OD |
∴CF=
| 20 |
| 3 |
(3)过点D作DM⊥AB于M,
∴DM=
| 3•4 |
| 5 |
| 12 |
| 5 |
又∵△ODM∽△OBD,
∴OM=
| 9 |
| 5 |
∴tan∠BAD=
| DM |
| AM |
| ||
|
| 6 |
| 17 |
点评:本题综合考查了相似三角形,勾股定理,垂径定理等相关知识,本题难度偏难.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
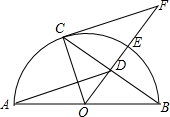
 交OE的延长线于点F.BC=8,DE=2.
交OE的延长线于点F.BC=8,DE=2.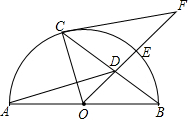 如图,AB是半圆O上的直径,E是
如图,AB是半圆O上的直径,E是