题目内容
 如图,点P是∠AOB的角平分线上一点,过P作PC∥OA交OB于点C.若∠AOB=60°,OC=4,则点P到OA的距离PD等于
如图,点P是∠AOB的角平分线上一点,过P作PC∥OA交OB于点C.若∠AOB=60°,OC=4,则点P到OA的距离PD等于2
| 3 |
2
.| 3 |
分析:过P作PM⊥OB于M,推出PD=PM,根据角平分线定义和平行线性质求出∠POC=∠CPO,推出OC=PC=4,求出∠CPM=30°,求出CM长,根据勾股定理求出PM即可.
解答:解:过P作PM⊥OB于M,
∵OP平分∠AOB,
∴∠AOP=∠BOP,
∵PC∥OA,
∴∠AOP=∠CPO,∠PCB=∠AOB=60°,
∴∠POC=∠CPO,∠MPC=90°-60°=30°,
∴PC=OC=4,
∵∠MPC=90°-60°=30°,
∴CM=
PC=2,
在△PCM中,由勾股定理得:PM=
=2
,
∵OP平分∠AOB,PD⊥OA,PM⊥OB,
∴PD=PM=2
.
故答案为:2
.

∵OP平分∠AOB,
∴∠AOP=∠BOP,
∵PC∥OA,
∴∠AOP=∠CPO,∠PCB=∠AOB=60°,
∴∠POC=∠CPO,∠MPC=90°-60°=30°,
∴PC=OC=4,
∵∠MPC=90°-60°=30°,
∴CM=
| 1 |
| 2 |
在△PCM中,由勾股定理得:PM=
| PC2- CM2 |
| 3 |
∵OP平分∠AOB,PD⊥OA,PM⊥OB,
∴PD=PM=2
| 3 |
故答案为:2
| 3 |
点评:本题考查了等腰三角形性质,角平分线定义,平行线性质,勾股定理等知识点的运用,关键是综合运用这些性质进行推理,题目比较好,是一道综合性比较强的题目.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 63、如图,点P是∠AOB的平分线上的一点,作PD⊥OA,垂足为D,PE⊥OB垂足为E,DE交OC于点F.则在图中:
63、如图,点P是∠AOB的平分线上的一点,作PD⊥OA,垂足为D,PE⊥OB垂足为E,DE交OC于点F.则在图中: 24、如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
24、如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
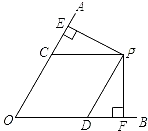 PF⊥OB,垂足分别为点E、F.
PF⊥OB,垂足分别为点E、F. 如图,点P是∠AOB内部一点,点P关于OA、OB的对称点是H、G,直线HG交OA、OB于点C、D,若HG=4cm,且∠AOB=30°,则△HOG的周长是
如图,点P是∠AOB内部一点,点P关于OA、OB的对称点是H、G,直线HG交OA、OB于点C、D,若HG=4cm,且∠AOB=30°,则△HOG的周长是