题目内容
1.计算:$\frac{1}{1×3}$+$\frac{1}{2×4}$+$\frac{1}{3×5}$+…+$\frac{1}{9×11}$=$\frac{36}{55}$.分析 先拆项为$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{9}$-$\frac{1}{11}$),再抵消得到$\frac{1}{2}$×(1+$\frac{1}{2}$-$\frac{1}{10}$-$\frac{1}{11}$),再计算即可求解.
解答 解:$\frac{1}{1×3}$+$\frac{1}{2×4}$+$\frac{1}{3×5}$+…+$\frac{1}{9×11}$
=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{9}$-$\frac{1}{11}$)
=$\frac{1}{2}$×(1+$\frac{1}{2}$-$\frac{1}{10}$-$\frac{1}{11}$)
=$\frac{1}{2}$×(1+$\frac{1}{2}$-$\frac{1}{10}$-$\frac{1}{11}$)
=$\frac{1}{2}$×$\frac{144}{110}$
=$\frac{36}{55}$.
故答案为:$\frac{36}{55}$.
点评 考查了有理数的混合运算,关键是熟悉$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$)的知识点.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
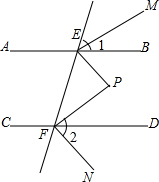 如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.∠1与∠2的平分线EM,FN,判断EM,FN所在的直线有什么位置关系,并说明理由.
如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线与∠DFE的平分线相交于点P.∠1与∠2的平分线EM,FN,判断EM,FN所在的直线有什么位置关系,并说明理由. 图中∠AED分别为△ADE,△ABE中AD,AB边所对的角,在△AFD中,∠AFD是边AF,ED组成的角.
图中∠AED分别为△ADE,△ABE中AD,AB边所对的角,在△AFD中,∠AFD是边AF,ED组成的角.