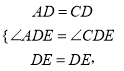题目内容
【题目】若![]() 是关于
是关于![]() 的函数,
的函数,![]() 是常数(
是常数(![]() ),若对于此函数图象上的任意两点
),若对于此函数图象上的任意两点![]() ,
,![]() ,都有
,都有![]() ,则称该函数为有界函数,其中满足条件的所有常数
,则称该函数为有界函数,其中满足条件的所有常数![]() 的最小值,称为该函数的界高.
的最小值,称为该函数的界高.
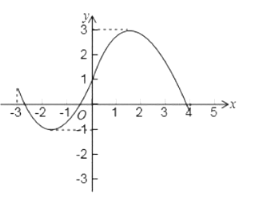
例如:下图所表示的函数的界高为4.
(1)求函数![]() 的界高;
的界高;
(2)已知![]() ,若函数
,若函数![]() 的界高为4,求实数
的界高为4,求实数![]() 的取值范围;
的取值范围;
(3)已知![]() ,函数
,函数![]() 的界高为
的界高为![]() ,求
,求![]() 的值.
的值.
【答案】(1) 界高为9;(2) ![]() ;(3)
;(3) ![]()
【解析】
(1)根据函数![]() (
(![]() )的性质,在
)的性质,在![]() 取最小值0,在
取最小值0,在![]() 取最大值9,由此可求函数的界高;
取最大值9,由此可求函数的界高;
(2)把![]() 代入抛物线的解析式得:
代入抛物线的解析式得:![]() ,解得
,解得![]() ,从而
,从而![]() ,进一步即得m的取值范围是
,进一步即得m的取值范围是![]() ;
;
(3)因为抛物线的对称轴是直线x=a,而![]() ,函数
,函数![]() 中的x的取值范围是
中的x的取值范围是![]() ,所以要对a分情况求解;
,所以要对a分情况求解;
当![]() 时,由二次函数的性质可知,函数在x=-2时,取得最大值,在x=1时取得最小值,将
时,由二次函数的性质可知,函数在x=-2时,取得最大值,在x=1时取得最小值,将![]() 代入函数解析式求得
代入函数解析式求得![]() ,然后根据
,然后根据![]() ,可求a的值;
,可求a的值;
当![]() 时,同样的思路将
时,同样的思路将![]() 代入函数解析式得
代入函数解析式得![]() ,再根据
,再根据![]() ,亦可求得a的值;最后综合得出结果.
,亦可求得a的值;最后综合得出结果.
解(1)函数![]() (
(![]() )在
)在![]() 取最小值
取最小值![]() ,在
,在![]() 取最大值
取最大值![]()
∵![]()
∴界高为9.
(2)将![]() 代入抛物线的解析式得:
代入抛物线的解析式得:![]() ,解得:
,解得:![]()
∴![]()
∴![]() 的取值范围是
的取值范围是![]()
(3)当![]() 时,由二次函数的性质可知,函数在x=-2时,取得最大值,在x=1时取得最小值,于是将
时,由二次函数的性质可知,函数在x=-2时,取得最大值,在x=1时取得最小值,于是将![]() 代入函数解析式求得
代入函数解析式求得![]() ,
,
∵![]()
∴![]()
解得:![]()
又∵![]()
故此种情况不成立;
当![]() 时,同理将
时,同理将![]() 代入函数解析式得:
代入函数解析式得:![]() ,
,
∵![]()
∴![]()
解得:![]() (舍去)
(舍去)
故![]()

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:![]() ):
):
第1批 | 第2批 | 第3批 | 第4批 | 第5批 |
|
|
|
|
|
(1)接送完第5批客人时,该驾驶员在公司什么方向,距离公司多远?
(2)若该出租车的收费标准为:行驶路程不超过![]() ,收费10元;超过
,收费10元;超过![]() ,对超过部分另加收每千米1.8元.当送完第5批客人时,该驾驶员共收到车费多少元?
,对超过部分另加收每千米1.8元.当送完第5批客人时,该驾驶员共收到车费多少元?